Chapters
When working with data in statistics, it’s not always easy to make sense of a long list of numbers. That’s where class intervals come in. They help us group data into manageable sections so we can see patterns more clearly.

What is a Class Interval?
A class interval is the range of values that belongs to a particular group (or “class”) in a frequency distribution table.
It is calculated as:
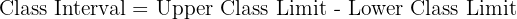
For example:
- If one class is 10–20, then
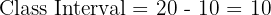
Why are Class Intervals Useful?
- Simplifies data: Instead of dealing with dozens (or hundreds) of individual numbers, data is grouped into ranges.
- Reveals patterns: It becomes easier to spot trends, such as which range of values is most common.
- Helps in graphing: Histograms and frequency polygons rely on class intervals to organize the data visually.
1. Find the range of the data: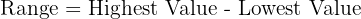
2. Decide how many classes you want: Usually between 5 and 20 depending on the size of your dataset.
3. Divide the range by the number of classes: 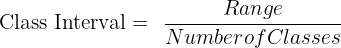
Practice Questions & Solutions
The ages of 10 students are:
{12, 15, 14, 13, 16, 17, 12, 18, 14, 15}
a) Find the range of the data.
b) If we want 4 classes, calculate the class interval.
Range = 18 − 12 = 6
Class Interval = 6 ÷ 4 = 1.5 → round up to 2
The marks scored by students in a test are:
{22, 35, 41, 28, 33, 48, 37, 44, 31, 39}
a) Find the range.
b) If we create 5 classes, what is the class interval?
Range = 48 − 22 = 26
Class Interval = 26 ÷ 5 = 5.2 → round up to 6
The heights (in cm) of 12 basketball players are:
{168, 172, 189, 175, 181, 177, 184, 190, 169, 173, 180, 176}
a) Find the range.
b) If we want 6 classes, what is the class interval?
Range = 190 − 168 = 22
Class Interval = 22 ÷ 6 ≈ 3.67 → round up to 4
*Extended Practice*
The following data are weights (kg) of people on a diet plan:
{52, 75, 92, 101, 83, 68, 133, 78, 104, 61, 39, 46, 135, 87, 131, 99, 104, 86, 67, 116, 89, 57, 87, 98, 131, 116, 135, 93}
a) Find the range of the data.
b) With a class interval of 14, determine how many classes you get.
c) Present these weights in a frequency distribution table.
Range = 135 − 39 = 96
Number of classes = 96 ÷ 14 ≈ 6.9 → 7 classes
| Class Interval | Frequency |
|---|---|
| 39–52 | 2 |
| 53–66 | 3 |
| 67–80 | 4 |
| 81–94 | 7 |
| 95–108 | 5 |
| 109–122 | 2 |
| 123–136 | 5 |
Key Takeaway
The class interval is simply the width of each group when organizing data into classes. It is essential in statistics for creating frequency tables, histograms, and understanding data trends.












How many class interval is there between 1 to 86
Hi Hritam,
That depends on how wide each class interval is.
The number of class intervals = Range/Class interval width
where
Range = Highest value – Lowest value = 86-1= 85
Class interval width = whatever size you choose (e.g., 5, 10, etc.).
For example:
If the interval size is 5 → 85÷5=17 intervals.
I like it please continue to teach me I’m a student
Not good better learn you only
for a set of raw data with the range of 99, how many class intervals could be formed if the class size is 10
Need help
With a class interval of 14, determine how many classes you will get from given list of midterm scores received by 50 students in a programming class:
45, 85, 92, 99, 37, 68, 67, 78, 81, 25,
97, 100, 82, 49, 54, 78, 89, 71, 94, 87,
21, 77, 81, 83, 98, 97, 74, 81, 39, 77,
99, 85, 85, 64, 92, 83, 100, 74, 68, 72,
65, 84, 89, 72, 61, 49, 56, 97, 92, 82