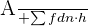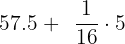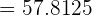To compute the single highest occurring score or the most frequently occurring scores in a raw data set, researchers employ stem- and - leaf plots, statistical programs, database management programs, or count by hand. All quantitative studies generate raw numerical data. Researchers convert data from qualitative studies into categories that can be then counted as frequencies. In descriptive statistics, the mode is of utmost importance, however, it does not make inferences or predictions about the data frequency in a population. It just gives us the relevant information about the specific sample. The other measures of central tendency are mean and median. In this article, we will answer frequently asked questions about this measure. So, let us get started.
How do you work out the modal class interval?
You can understand the meaning of modal class interval by examining the meaning of each term in the phrase. Modal means the one that occurs most often (averages: mode). In maths, the mode is one of the most common ways to describe a set of data. A class interval is the width of one of your groups in the frequency table or, the class interval is what you use when grouping data together. The modal class is, therefore, the group with the highest frequency. For example: if you counted the number of pencils in different pencil cases and you decided to group them. You might record how many pencil cases had 1 to 5 pencils in, how many had 6 to 10 pencils in, how many had 11 – 15 pencils, etc, up to whatever number is practical. In this example, your class intervals are:
- 1 – 5 pencils, 2 pencil cases
- 6 – 10 pencils, 4 pencil cases
- 11 – 15 pencils, 6 pencil cases
- 16 – 20 pencils, 1 pencil case.
If you found that there were more pencil cases with 11 – 15 pencils in than any other class interval, then 11 – 15 is your modal class interval.
What is the modal interval?
Mode refers to a value that is frequently repeated in a data set. In other words, this value occurs more often in a data set. Mode is often used to describe a data set. The width of the group in the frequency table is known as a class interval. The modal interval is a class interval with the highest frequency. For instance, consider the following data set which shows the number of students in a class divided by age group.
| Group | Age group | Number of students |
| 1 | 4-5 | 12 |
| 2 | 6-7 | 11 |
| 3 | 8-9 | 6 |
| 4 | 10-11 | 10 |
| 5 | 12-13 | 8 |
| 6 | 14-15 | 4 |
You can see in this table, that the class interval with the highest frequency is 4-5. Hence, this is a modal interval.
What is a modal class in statistics?
Now, we will answer what is modal class in math or statistics. Modal class in statistics refers to a class having the highest frequency. It refers to a class in which the frequency is the highest in a continuous quantitative statistical variable distribution in which the values are grouped into classes with similar dimensions. The mode is not widely used as a measure of central tendency for continuous quantitative variables because it is more helpful for qualitative variables as mean and median do not make sense in such variables. To compute the mode of the distribution of grouped data, the middle range of the modal class is used.
How do you calculate modal class?
Modal class is the class interval with the highest frequency. Consider the following example:
| Score range | Number of students |
| 60-65 | 11 |
| 65-70 | 13 |
| 70-75 | 6 |
| 75-80 | 10 |
| 80-85 | 9 |
In the above example, the modal class is 65-70 because it has the highest frequency. Let us see how we can compute mode for the above grouped data. The formula for mode is given below:
Mode = 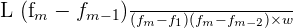
- L is the lower class boundary of the modal class
- fm-1 refers to the frequency of the group before the modal class
- fm refers to the frequency of the modal group
- fm+1 refers to the frequency of the group after the modal group
- w is the width of the class intervals
Substitute the values from the table in the above formula as shown below:
Mode = 
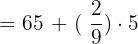
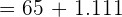

You can also calculate median and mean from the grouped frequency table.
How do you find the class interval?
Consider the following data set which shows the weight of students in a class in kilograms:
55, 45, 48, 56, 69, 48, 54, 55, 45, 53, 55, 58, 62, 65, 68, 70
Follow these steps to define the class interval:
- To find the class interval, which depicts the range of data for each group, the first thing you have to do is to decide how many classes, or groups of data you need. For instance, you have decided that you need 5 classes for data.
- The next step is to work out the difference between the highest and lowest value. The highest weight in the above data set is 70 and the lowest weight is 45. Their difference is 70 - 45 = 25.
- Now, divide this number 25 by 5 to get 5. This means that our class width will be 5.
Using the above steps, we can group the data into different class intervals like this:
| 45-50 | 4 |
| 50-55 | 1 |
| 55-60 | 5 |
| 60-65 | 2 |
| 65-70 | 4 |
How to work out the mean from a grouped frequency table?
Consider the table from the previous question which shows the weight of students in a class:
| 45-50 | 4 |
| 50-55 | 1 |
| 55-60 | 5 |
| 60-65 | 2 |
| 65-70 | 4 |
As this is a grouped data, so we will use the formula to compute the mean of the grouped data. The formula for the mean of the grouped data is given below:
Mean = 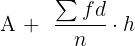
Here: A = mid value of modal class n refers to the number of observations f is the frequency d = 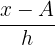 , where x is the average of the highest and lowest class interval, A is the mid value of the modal class, and h is the number of class intervals. We will work out f x d for each class interval and take its sum as shown in the table below:
, where x is the average of the highest and lowest class interval, A is the mid value of the modal class, and h is the number of class intervals. We will work out f x d for each class interval and take its sum as shown in the table below:
| Class Interval | Frequency (f) | Mid value (x) | d | f x d |
| 45-50 | 4 | 47.5 | -2 | -8 |
| 50-55 | 1 | 52.5 | -1 | -1 |
| 55-60 | 5 | 57.5 = A | 0 | 0 |
| 60-65 | 2 | 62.5 | 1 | 2 |
| 65-70 | 4 | 67.5 | 2 | 8 |
| n = 16 | | | sum = 1 |
Now, we will substitute the values in the formula to get the value of the mean.
Mean = 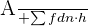
Mean = 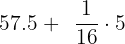
Mean = 
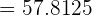


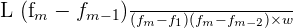

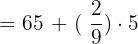
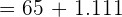

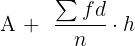
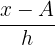 , where x is the average of the highest and lowest class interval, A is the mid value of the modal class, and h is the number of class intervals. We will work out f x d for each class interval and take its sum as shown in the table below:
, where x is the average of the highest and lowest class interval, A is the mid value of the modal class, and h is the number of class intervals. We will work out f x d for each class interval and take its sum as shown in the table below: