Many pupils find it challenging to embrace abstract concepts like maths. Particularly when learners are very young, they have no real understanding of what maths is. They've yet to see what maths represents.
'Bar method maths' makes mathematics real. Pupils can see the maths, and make it happen, too. Children can relate to a bar model because it gives them more information than abstract symbols like numbers, +, and ÷.
What is the Bar Method in Maths?
- It's a system for making maths visible and relatable
- It helps learners develop a relationship with maths
- It guides pupils to understand the relationship between maths and the real world
- Modelling helps learners build numbers sense and problem-solving skills.

What Is a Bar Model?

Visual representations of numerical values are so common we forget how prevalent they are. For example, every smartphone has two bar graphs in their upper right-hand corners.
One represents signal strength, and the other shows the percentage of battery charge left. The more bars your signal graph has, the stronger your reception.
Chief Executive Officers (CEOs) read bar models that represent company data. They don't have time to plod through all their accountants' and engineers' equations in search of results. They need a quick visual of the company's bottom lines, preferably in colour.
Bar graphs help CEOs decide which company initiatives to prioritise. They help smartphone users estimate how much longer they can use their devices before having to recharge them. In maths classrooms, the same principles guide learners to the answers they need.
Bar models are not calculators. They will not do pupils' maths computations. Instead, they give students an easy way to decide which calculation they should do, to solve the problem.
One might argue that, especially in the early stages of maths learning, pupils accept a lot on faith. They find no logic behind the symbol 5 being more, or bigger, than 2. Especially not when it looks like the numbers are the same size.
For Early Years Foundation Stage (EYFS) and Key Stage 1 (KS1) students, one symbol is as good as the next. So, introducing bar modelling as early as possible gives learners visual proof of symbols' meanings.
It's a visual representation of one or more numerical values.
Modelling maths problems with bar models is a fundamental part of the Singapore Maths CPA process. CPA stands for Concrete, Pictorial, Abstract.
The concrete phase calls for learners to manipulate items to represent numerical values. Creating bar models is this process' pictorial phase. This phase helps pupils connect what's actual and visible to abstract maths concepts.
Bar Models and Their Uses
CEOs and phone batteries aside, we find many uses for bar models in maths classrooms. Across the UK, students of all levels use bar models to estimate maths problem results. Pupils can use them to model basic arithmetic equations, fractions, and percentage problems.
Modelling word problems is a particularly good use for bar models. Often, such questions present confusing scenarios, with important information disguised amid unhelpful facts. To model word problems, pupils must first highlight what's important. And then, they can model what they know, to solve for the unknown value.
1. To organise information.
2. To represent a maths problem visually.
3. To estimate answers to maths problems.
4. To decide which calculation will solve the problem.
5. To solve word problems.
This maths learning strategy offers more than one bar model. Each is ideal for a particular type of maths operation, though sometimes, they are interchangeable.
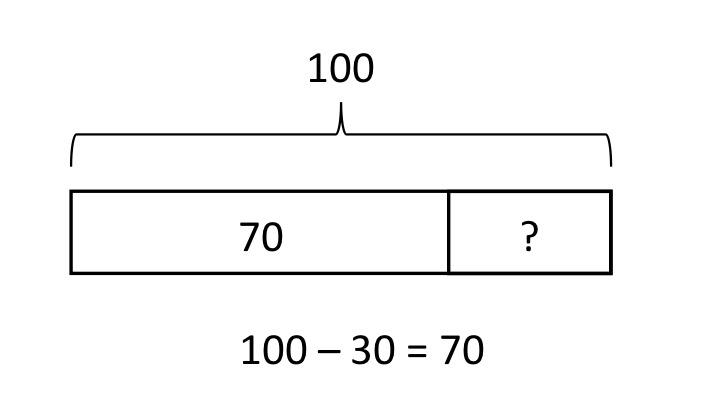
- The Part-Whole Model
- also called 'part-part-whole'
- best for answering 'missing number' questions
- typically used for arithmetic problems
- can be used for other applications
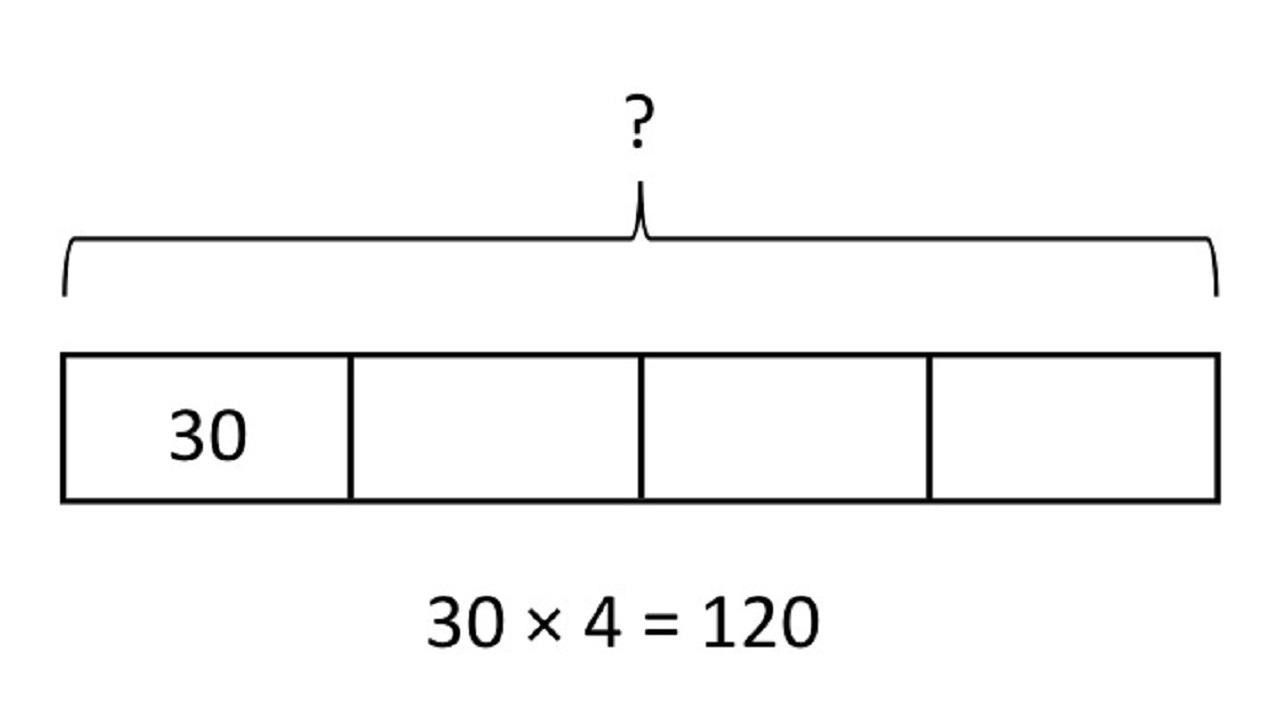
- The Equal Parts Model
- best for fractions
- excellent for percentages
- can also be used for multiplication
Students must use the right bar model for the operation they work on. Furthermore, they must make sure their models correctly represent the given values. For instance, to model 8 + 4 = ?, the '8' box must be twice as large as the '4' box.
Other Bar Model Types
The Comparison Model typically consists of two or more bars, one below the other, that represent different values. This type of model helps learners compare quantities, to calculate the difference between them. These bar models are great for ratio and proportion questions.
They're perfect for more advanced equations that pupils work on in KS2 maths classes, and beyond. Learners often have difficulties transitioning into concepts like algebra and geometry. Comparison bar models remind them that, if the equation can be seen, it can be solved - even if they're solving for X.
Word problems are where comparison bar models deliver. As noted above, these questions contain a lot of extra information that cloud the maths issue. By modelling these problems, students get to the heart of the equations. Once they know what they must solve for, it's only a matter of choosing the right operation, and executing it.
Fractions are equally challenging for pupils to master. However, fraction bar models make such maths problems easy to understand. As fractions represent equal parts of a whole amount, we might consider fraction models to be Equal Part models.
All of these bar models fit within the Singapore Maths mastery system. Like their pupils, teachers must decide which bar model to use when introducing new maths concepts. So, it's a good idea to distinguish between the models. In our next chapter, you'll find examples for each type.
Problem-Solving With a Bar Model Example
As early as Year 1, pupils confront word problems. They're typically very simple, and revolve around arithmetic. Bar models are valuable tools to help pupils separate the maths operation from the text.
Here, we have a standard addition word problem for this learning level.
Together, Mark and John have 17 marbles. Eight of them belong to John. How many marbles belong to Mark?
Pupils must first highlight all the important information. The exercise poses a total of 17 (marbles), eight of which are accounted for. The question asks how many marbles are left?
Using the part-part-whole model, students can represent 'the whole', and one part. With that done, they can see that subtracting the known quantity (8) from the total gives them their answer.
Using the Equal-Part Model
Now, to use the equal-part model. And then, we will apply this model to a fraction word problem. This example shows us how to use it.
Part I:
Mary has five packs of stickers. Each pack contains 25 stickers. How many stickers does Mary have?
Part II:
Mary wants to share her stickers with all her classmates. Her class counts 25 pupils, including her. How many stickers will each student have?
Part I is straightforward; a part-whole model will reveal the calculation. However, Part II is tricky. It challenges the learner to decide whether Mary counts as a student who should also have stickers.
The key information is 'to share'. In other words: Mary will keep her portion of stickers. With that settled, students can write the equation to answer the question.

The Comparison Bar Model
The Smith family has three children. Thomas, the youngest, is eight years old. Jane is three years older than Thomas, and Siobhan is two years older than Jane. What is the total age of the Smith children?
Answering this question requires three bars. The first, relatively short bar, represents Thomas. Jane will have a bar with a part as long as her brother's, and a bit longer, for the extra 3 years. Siobhan's bar will include Thomas' and Jane's parts, and one more part, for the added two years.
You can discover more bar model example solutions about how to apply bar models to specific problems in our companion article. You may also find this video helpful.
How to Include Bar Method Maths In Class
Teachers in the UK have plenty to do. They have reports to fill out and file, and assessments to conduct. They must grade papers and check homework. All that is on top of teaching new concepts, and reinforcing previously learned ones. A complete maths tutor can provide additional support to ease their workload.
Does adding a new feature help or hinder teachers' efforts? Regardless of how you feel about the topic, Singapore Maths and bar models are now integral to how we teach maths.
Admittedly, the burden falls more heavily on primary school teachers. They first introduce the concept of modelling, and must put in the work to make sure students model correctly.
Part-part-whole bar models suit practically every primary school maths application. So, it makes sense to teach that type of model first. You may model arithmetic problems, as well as word problems. Especially word problems, as those are the most challenging for your students.
Towards the end of KS1, teachers might make more use of comparison bar models. That's when word problems get more complex. Modelling those exercises reinforces the practice of eliminating the unnecessary information such problems typically contain.
Following these tips makes your teaching more extensive, and more thorough. It ensures that your students come away with a deeper understanding of maths concepts. It also gives them the tools to think critically.
This overview of Singapore Maths bar modelling paves the way for students to understand and work with abstract maths concepts. It also encourages them use logic, not just to solve maths problems, but in their everyday thinking.
Bar models make...















