Singapore maths has been a part of the UK maths curriculum for 15 years. Our Department for Education (DfE) launched the initiative in 2009, and set up teacher support systems to make the rollout successful. Despite their efforts, the carry-through has been uneven.
As you read this, most UK maths classrooms use Singapore Maths to teach new concepts. Many teachers have been through the Maths Hubs training programme, and rely on that platform for support. Many, but not all. This series of articles is for teachers not yet in this loop, and for parents who want to know more about Singapore maths.
Key Aspects of Singapore Maths
- It is a system for making maths relatable to students
- It comprises three components: concrete, pictorial, and abstract (CPA)
- Students use bar models to diagram all types of maths problems
- The Singapore Maths method helps learners build problem-solving and critical thinking skills

What Is Singapore Maths?
All things considered, Singapore Maths is neither revolutionary, nor extraordinary. It represents the best of mathematical thinking - logical, and methodical. It's maths learning as it always should have been.
Maths is an abstract discipline. We all must agree on what its symbols represent, including the symbols that represent numbers. For young minds, it takes some time to accept that 3 is half of 6, especially if those numbers appear in the same font size.
That's why giving the youngest students visual proof of numerical concepts is so important. It helps them develop numbers sense - the order of numbers, and their relationship to each other. Without that, maths learning cannot succeed. That is the foundation of Singapore Maths.
How Singapore Maths Developed
The country of Singapore gained its independence from Malaysia in 1967. The new nation had to establish and build all the systems of a functioning society. Those include hospitals and schools, as well as government agencies. And, they had to secure the materials to keep their society running.
Education was a high priority, so government officials imported textbooks to keep the schools going. Teachers used those books for around 20 years, until the government had the means to produce their own books. And then, amazing things started happening.
1982
Singapore produces its first maths textbook
It was called Primary Mathematics
1992
Singapore revises its maths textbook
To place emphasis on problem-solving, rather than memorising maths facts.
1995
Singapore maths students top global rankings for maths scores for the first time.
They do so again in 1999 and 2003 (also, in 2015).
2005
US education specialists study Singapore's maths instruction methods.
US schools adopt this maths instruction method.
2009
The UK DfE embraces Singapore Maths
This department launches the Maths Hubs initiatives to train teachers.
In its most basic and concrete terms, we can define Singapore Maths as a system to improve students' maths outcomes. However, that explanation is far too narrow to cover all that this learning method is and does. We need a deeper dive to get the whole picture.
Why It's Called Singapore Maths
In fact, this problem-solving strategy goes by many names. Method math, for instance. Or, in Australia, Mathematical Methods. Regardless of name, all these strategies revolve around the same principles. They are problem-solving, reasoning, logic, and maths fluency.
The US authorities investigated these principles in 2005. They gave this system that name to distinguish it from other maths initiatives.
Singapore Maths: the CPA Method
This maths mastery system uses a three-step process that lets students 'see' the maths they do. It's called CPA, which stands for Concrete, Pictorial, Abstract. During the Concrete phase, learners touch and arrange objects to represent maths equations.
From this hands-on exercise, pupils transition into more abstract maths representations. The same equation they arranged objects for will now be addressed on paper.

They will draw visual representations of it, replacing concrete items with abstract symbols. This is the pictorial phase, which usually involves bar models of equations.
Educational theory has long suggested that students have 'learning styles' - visual, hearing, or moving and touching. The Singapore Maths CPA method involves these senses.
Since around 2012, educational theorists reject the idea that learners are either visual, auditory, or kinaesthetic. They advocate for abandoning the 'learning styles' theory. They insist that all humans learn using all their senses, and that we shouldn't categorise pupils by their learning preferences.
The CPA approach maths system seems to support that idea. All students will manipulate objects. All learners will draw bar models. All pupils will listen to instructions, and speak out their answers.
The Point of CPA
Children learn by manipulating objects ...
Jean Piaget
Pioneering educational theorists like Jean Piaget and Maria Montessori based their teaching models on 'learn through play' ideas. They noted, through their studies, that even small children can experiment and draw conclusions. Such 'play' trains learners to think logically and critically.
That's the point of CPA in Singapore Maths. It empowers students to use all their faculties to understand abstract maths concepts. It places no emphasis on memorising maths facts - times tables, order of operations (BODMAS), and so on.
Through ways of working with maths information, learners internalise those rules. Teachers no longer need to drill in these maths concepts. Those rules become a natural part of pupils' abilities to think mathematically.
What to Know About Bar Modelling
Bar modelling means turning concrete CPA exercises - the manipulation phase, into representations on paper. In other words, it means translating what students did with the objects in their hands into a drawing in their notebooks.
Bar modelling is the Singapore Maths method's most lasting phase. Long after students stop needing concrete models, they will still use bar models to organise maths information. Typically, this happens around the end of Key Stage 2 (KS2), though some learners rely on concrete representations beyond that point.
Bar modelling helps students organise information found in their maths exercises.
Students have three types of bar models to choose from, but they all serve the same purpose.
- These models help students decide what information is important.
- Bar models allow learners to organise information.
- Modelling guides pupils to the mathematical operations they need.
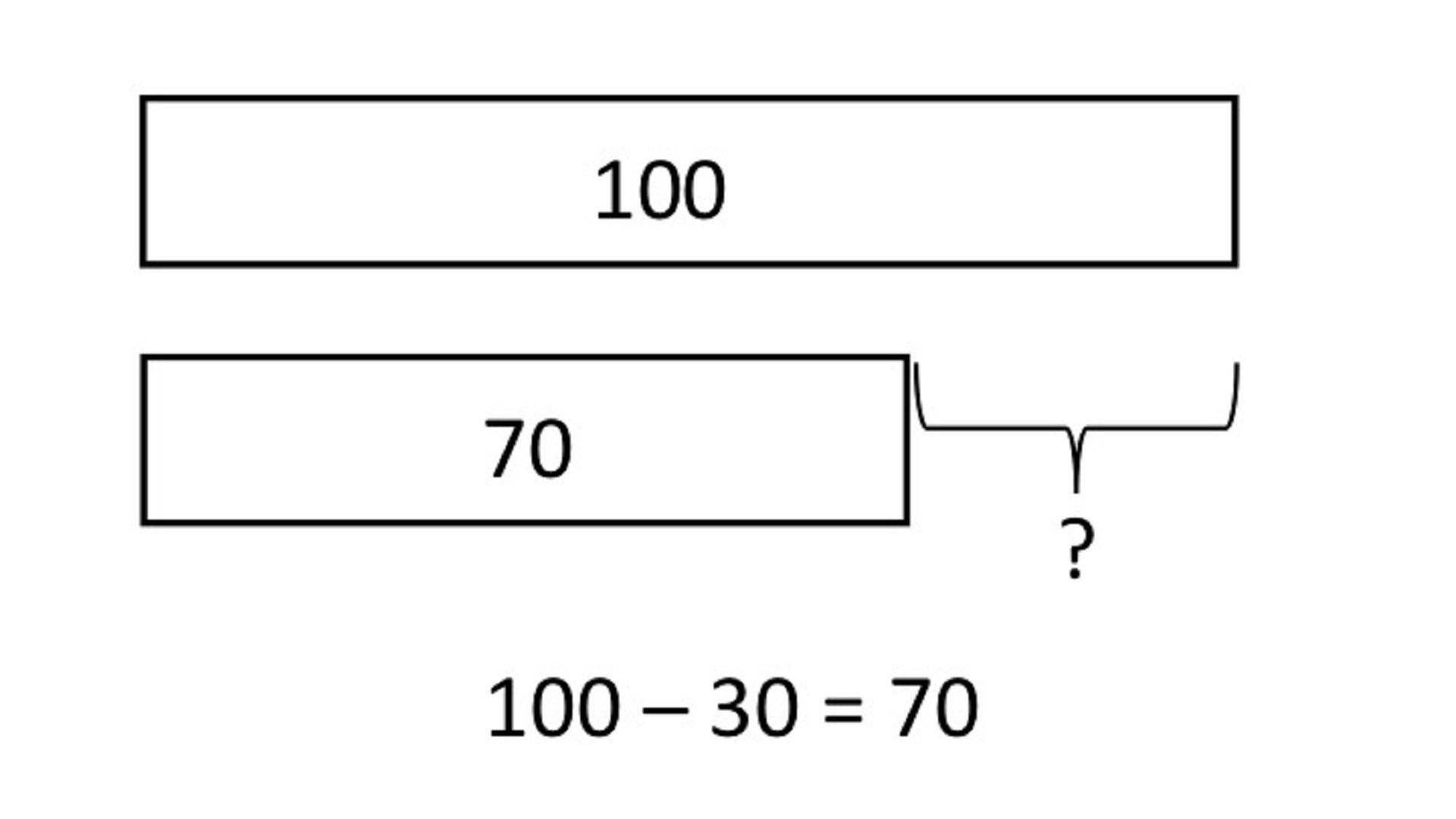
Bar models are particularly useful for solving word problems. Often, this type of maths exercise includes a lot of facts that have nothing to do with maths. Also, they cloud the maths information students need to set up and solve their equations. Consider, for instance, this word problem:
Jack, Martin, and William went fishing. Altogether, the boys caught 11 fish. William caught three fish, and Martin caught twice the number. Did Jack catch more, or fewer fish than the other boys?
This problem calls for multiplication, addition and subtraction, and demands estimation. Learners must choose from one of these three models to satisfy all of this exercise's requirements.
Part-Part Whole Model
- ideal for arithmetic questions
- defines known and unknown values
- indicates which operation(s) to use
Comparison Model
- helps to compare values
- helps to estimate results
Equal Parts Model
- best for fractions
- ideal for percentages
Students know that bar modelling is the best way to approach such exercises as the one above. To answer that question, they would rely on the part-part-whole model. Modelling that problem guides them to all the solutions the problem demands.
Bar Modelling for Specific Maths Problems

KS 1 pupils might find exercises like the one above in their workbooks. However, bar modelling works for higher and lower level classes, too. Even Year 1 learners have word problems to model and solve.
Secondary school mathematics is easier to manage with these tools, too. For example, how would a Year 10 learner model this problem, from the AQA Maths 2023 GCSE exam?
A shop sells pens for 24 pence, and calculators for £7. This week, the shop is running a sale. Pens are 1/4 off the normal price, and calculators are 30% off. How much will you pay if you buy 5 pens and 1 calculator?
The student who thinks mathematically would follow these steps:
- highlight all the important information
- decide on the proper bar model for these calculations
- organise the information
- populate the model with the given information
- solve the problem
As this question gives fractions and percentages, the student selects the equal-part model. They draw one bar with four boxes to represent the pens, and one with 10 boxes for the calculator. From there, they will:
Pens
- divide the pen's price by 4
- subtract that result from the pen's original price
- multiply that answer by five
Calculator
- divide the price by 10
- multiply that value by 3
- subtract that result from the original price
Their final step is to add the results from both models. That reveals what the shopper paid for those items.
Choosing the right bar model for each question boosts students' mathematical thinking abilities. They won't need to try and discard each model until they happen on the right one.
They visualise how they must do the work, and know just what they need to do it. Developing this maths ability is the greatest benefit of Singapore Maths.
























