Linear programming is a method used in mathematics to achieve the best possible outcome in a given situation—typically maximising or minimising a quantity such as profit, cost, or time—while working within a set of constraints. For A-Level Maths, linear programming appears in the Decision Mathematics module (also known as D1 or D2 in some exam boards), and is often presented through real-life scenarios involving resource allocation, budgeting, production limits, and transportation planning.

📝 Linear Programming Practice Questions
1. Defining decision variables (e.g. number of items produced)
2. Formulating a linear objective function to maximise or minimise
3. Writing a set of linear inequalities that represent constraints
4. Graphing the feasible region and identifying possible solutions
5. Using a corner-point or vertex-testing method to find the optimal solution
A transport company has two types of trucks, Type A and Type B. Type A has a refrigerated capacity of  and a non-refrigerated capacity of
and a non-refrigerated capacity of 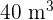 . In contrast, Type B has the same overall volume with equal refrigerated and non-refrigerated stock sections. A grocer must hire trucks to transport
. In contrast, Type B has the same overall volume with equal refrigerated and non-refrigerated stock sections. A grocer must hire trucks to transport 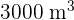 of refrigerated stock and
of refrigerated stock and 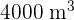 of non-refrigerated stock. The cost per kilometre of Type A is
of non-refrigerated stock. The cost per kilometre of Type A is  , and
, and  for Type B. How many trucks of each type should the grocer rent to achieve the minimum total cost?
for Type B. How many trucks of each type should the grocer rent to achieve the minimum total cost?
a) Choose the unknowns.
x = Type A trucks
y = Type B trucks
b) Write the objective function.
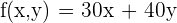
c) Write the constraints as a system of inequalities.
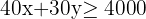
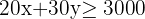


d) Find the set of feasible solutions that graphically represent the constraints.
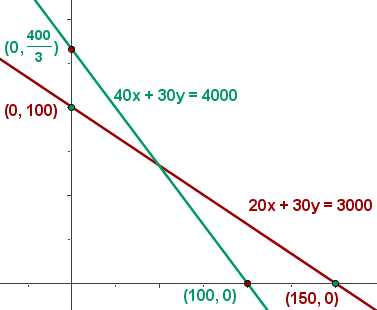
e) Calculate the coordinates of the vertices from the compound of feasible solutions.

f) Calculate the value of the objective function at each vertex to determine which has the maximum or minimum values.
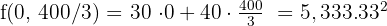
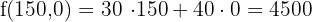
As x and y must be natural numbers round the value of y.
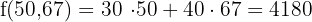
By default, we see what takes the value x to y = 66 in the equation 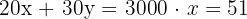 , which is within the feasible solutions.
, which is within the feasible solutions.
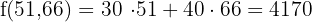
The minimum cost is 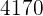 . To achieve this 51 trucks of Type A and 66 trucks of Type B are needed.
. To achieve this 51 trucks of Type A and 66 trucks of Type B are needed.
A school is preparing a trip for 400 students. The transportation company has 10 buses of 50 seats each and 8 buses of 40 seats but only has 9 drivers available. The rental cost for a large bus is 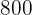 and
and  for a small bus. Calculate how many buses of each type should be used for the trip for the least possible cost.
for a small bus. Calculate how many buses of each type should be used for the trip for the least possible cost.
a)Choose the unknowns.
x = small buses
y = big buses
b) Write the objective function.
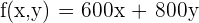
c) Write the constraints as a system of inequalities.
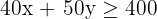

d) Find the set of feasible solutions that graphically represent the constraints.
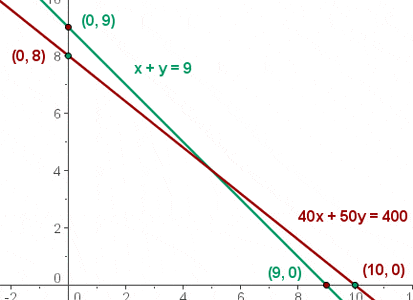
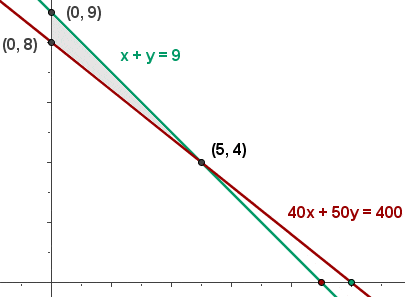
e) Calculate the coordinates of the vertices from the compound of feasible solutions.
f) Calculate the value of the objective function at each vertex to determine which has the maximum or minimum values.
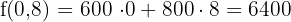
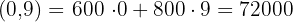
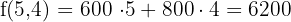
Hence, the minimum cost is 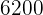 . This is achieved with 4 large and 5 small buses.
. This is achieved with 4 large and 5 small buses.
We substituted the points (0,9), (0,8), and (5,4) in the equation to determine the minimum cost. However, you can tell this by directly looking at the graph. The coordinate (5,4) comes under the feasible region and is the minimum point of it.
A store wants to liquidate 200 shirts and 100 pairs of pants from last season. They have decided to create two promotional offers, A and B.
Offer A includes one shirt and one pair of pants, and sells for 30.
Offer B includes three shirts and one pair of pants, and sells for 50.
The store does not want to sell fewer than 20 packages of Offer A or fewer than 10 packages of Offer B. How many packages of each offer should the store prepare in order to maximise total sales revenue from the promotion?
a) Choose the unknowns.
x = number of packages of Offer A
y = number of packages of Offer B
b) Write the objective function.
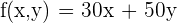
c) Write the constraints as a system of inequalities.
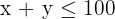



d) Find the set of feasible solutions that graphically represent the constraints.

Example 3 - part d
e) Calculate the coordinates of the vertices from the compound of feasible solutions.

Example 3 - part e
f) Calculate the value of the objective function at each vertices to determine which has the maximum or minimum values.
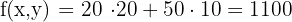
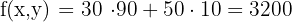
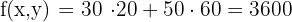
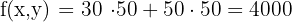
50 packages of each offer generate a maximum of 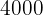 in sales.
in sales.
🔹 Steps for Solving Linear Programming Problems
To solve a linear programming problem effectively, follow these key steps. These are the standard methods used at A-Level for two-variable problems that can be solved graphically.
1. Define the decision variables
Start by identifying what the problem is asking you to find. Usually, this involves quantities such as the number of units produced or hours allocated. Assign variables (typically x and y) to represent these unknowns.
Example: Let x be the number of tables produced, and y the number of chairs.
2. Write the objective function
The objective function is the formula you want to maximise or minimise—often profit, cost, or time. It will usually be a linear equation in terms of x and y.
Example: Maximise profit
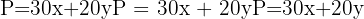
3. Formulate the constraints
Write out the inequalities based on the problem's limitations—such as time, materials, or budget. These are the conditions the solution must satisfy. Also, include non-negativity constraints x≥0x \geq 0x≥0 and y≥0y \geq 0y≥0, since negative quantities often don’t make sense in real-world scenarios.
Example:
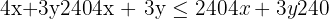 (material limit)
(material limit)
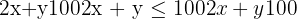 (labour limit)
(labour limit)
4. Draw the feasible region
On graph paper or using graphing software, plot each constraint as a straight line and shade the region that satisfies all the inequalities. The feasible region is the area where all constraints overlap.
5. Identify the corner (vertex) points
The maximum or minimum value of the objective function will occur at one of the corner points (vertices) of the feasible region. Find the coordinates of each vertex—either by observation, solving equations simultaneously, or using intersection points.
6. Evaluate the objective function at each vertex
Substitute the coordinates of each vertex into the objective function. Compare the results to determine the maximum or minimum value, depending on what the question asks.
Example:
Test
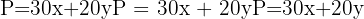 at each vertex and identify the one that gives the highest profit.
at each vertex and identify the one that gives the highest profit.
7. State the final solution clearly
Write out the optimal values of x and y, and what they represent in context (e.g. number of items to produce), along with the maximum or minimum value of the objective function.
These concepts combine algebra, graphical representation, and logical reasoning—making linear programming a valuable tool not only in mathematics exams but also in solving practical problems in business, science, and industry.
In the exercises below, you’ll find word problems typical of A-Level assessments, each followed by a fully worked solution. These will help you understand how to model real-life situations mathematically, interpret inequalities, and apply systematic methods to find optimal results.
Summarise with AI:












GOOD PRESENTATION. DO YOU HAVE ONE ON COORDINATE GEOMETRY?
Thanks so much! I’m really glad you liked the presentation. Yes — we actually do have a great set of resources on coordinate geometry. You can find them here:
👉 https://www.superprof.co.uk/resources/academic/maths/geometry/
The language in the third question is confusing. “Offer A is a package of one shirt and a couple of pants which will sell for “. A couple of pants indicate 2 pants instead of a single pair of pant, it could’ve been renamed as a pair of pant. Couple of pant”s” means plural. Please change the language. From my understanding, the offer A consisted of 1 shirt and 2 pants, but in the solution, they have considered one shirt and one pant.
Thank you for your feedback! You’re absolutely right — the wording around “a couple of pants” was confusing. The problem has now been updated to clearly state that Offer A includes one shirt and one pair of pants, which aligns with the solution provided. We appreciate you taking the time to point this out and helping us improve the clarity of the question.
it can be nice when you help me to pass
Hi Matovu! Thank you for your comment! Wishing you best of luck with your studies!
Hi there, thanks for your comment and for taking the time to share your calculation!