Chapters

What is Linear Programming?
Linear programming (LP) is a method of optimisation. It is used when we want to maximise or minimise a quantity (such as profit, cost, or time) while working under certain constraints (such as limited resources, time, or materials).
In LP:
- The unknowns are called decision variables.
- The formula to optimise is called the objective function.
- The limits or rules are expressed as linear inequalities or equations called constraints.
The solution is the set of values for the decision variables that gives the best result while satisfying all constraints.
Why is Linear Programming Important?
Linear programming is important because it helps us make the best possible decision when resources are limited. It is widely used in:
- Business & Economics – to maximise profit or minimise costs.
- Manufacturing – to decide the best mix of products with limited resources.
- Transportation & Logistics – to minimise delivery costs or times.
- Energy & Engineering – to optimise resource allocation and system design.
In short, LP provides a systematic way to achieve efficiency and avoid waste.
1. Decision Variables – the unknowns we want to solve for (e.g. number of products).
2. Objective Function – the quantity to maximise or minimise.
3. Constraints – the rules or limits written as linear inequalities/equations.
4. Non-Negativity – variables must be greater than or equal to zero.
5. Feasible Region – the set of all possible solutions that satisfy every constraint.
Steps to Solve a Linear Programming Problem
- Define the decision variables
Decide what x and y represent. - Write the objective function
Express the quantity to optimise (e.g. profit) as an equation. - Write the constraints
Translate the problem conditions into inequalities. - Choose a solution method
- Graphical method (for 2 variables) – plot the constraints and find the feasible region.
- Simplex method or software tools (for larger problems).
- If using the graphical method:
- Plot the constraints and shade the feasible region.
- Identify the corner points (vertices) of the feasible region.
- Evaluate the objective function at each corner point.
- Select the best solution (maximum or minimum value, depending on the problem).
Worked Example: Bakery Problem
Problem:
A bakery makes caramel cookies (x) and chocolate chip cookies (y):
- At least 80 caramel and 120 chocolate chip must be made daily.
- At most 120 caramel and 140 chocolate chip can be made.
- At least 240 cookies in total must be produced daily.
- Profit: $1 per caramel, $0.88 per chocolate chip.
How many of each cookie should be made to maximise profit?
Step 1 – Decision Variables
x = caramel cookies
y = chocolate chip cookies
Step 2 – Objective function
P = 1x + 0.88y
Step 3 – Constraints
x ≥ 80
x ≤ 120
y ≥ 120
y ≤ 140
x + y ≥ 240
x, y ≥ 0
Step 4 – Draw the graph

Step 5 – Identify corner points
(100,140), (120,120), (120,140)
Step 6 – Evaluate
P(100,140)=223.2
P(120,120)=225.6
P(120,140)=243.2
Step 7 – Best solution
Maximum profit = $243.20, at 120 caramel and 140 chocolate chip cookies.
Practice Questions (with Solutions)
A shop makes chairs (x) and tables (y). Calculate the maximum profit given the below constraints:
Chair: 2 hrs carpentry, 3 hrs painting.
Table: 3 hrs carpentry, 2 hrs painting.
Max: 60 carpentry hrs, 48 painting hrs.
Profit: $30 per chair, $40 per table.
Step 1 – Define variables
x = number of chairs
y = number of tables
Step 2 – Objective function
Maximise: P = 30x + 40y
Step 3 – Constraints
2x + 3y ≤ 60 (carpentry)
3x + 2y ≤ 48 (painting)
x, y ≥ 0
Step 4 – Draw graph
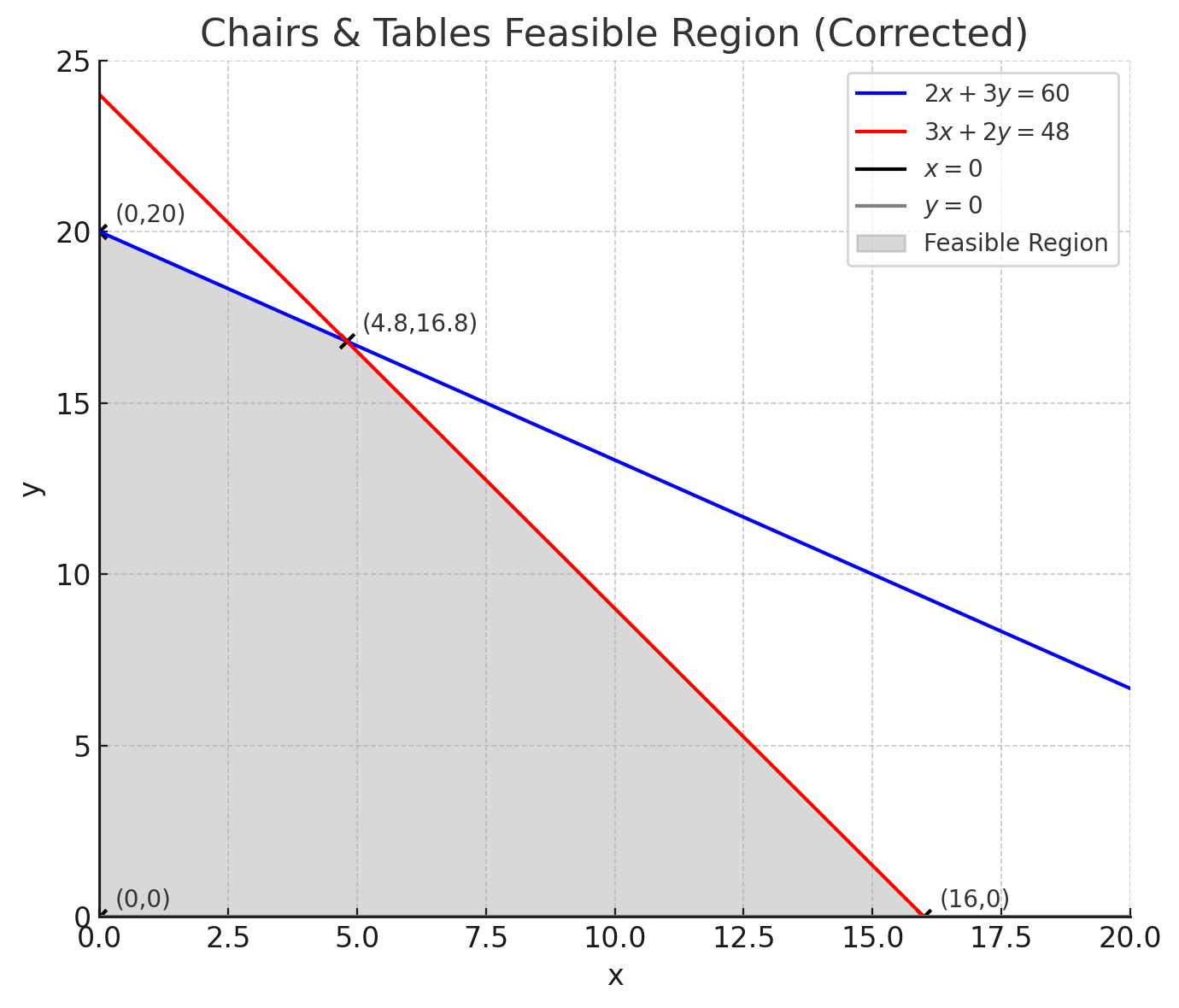
Step 5 – Corner points(0,0), (16,0), (0,20)
Intersection of 2x + 3y = 60 and 3x + 2y = 48 → (4.8,16.8). However, we cannot have fractional numbers of chairs and tables so this vertex can be discarded.
Step 6 – Evaluate objective function
P(0,0) = 0
P(16,0) = 480
P(0,20) = 800
Step 7 – Conclusion
Maximum profit = $800 at (x,y) = (0,20)
A factory makes products A (x) and B (y). Calculate the maximum profit given the below constraints:
A: 1 unit raw material, 3 hrs labour
B: 2 units raw material, 2 hrs labour
Available: 8 raw units, 12 labour hrs
Profit: $20 per A, $30 per B
Step 1 – Define variables
x = number of A
y = number of B
Step 2 – Objective function
Maximise: P = 20x + 30y
Step 3 – Constraints
x + 2y ≤ 8 (raw materials)
3x + 2y ≤ 12 (labour)
x, y ≥ 0
Step 4 – Draw graph
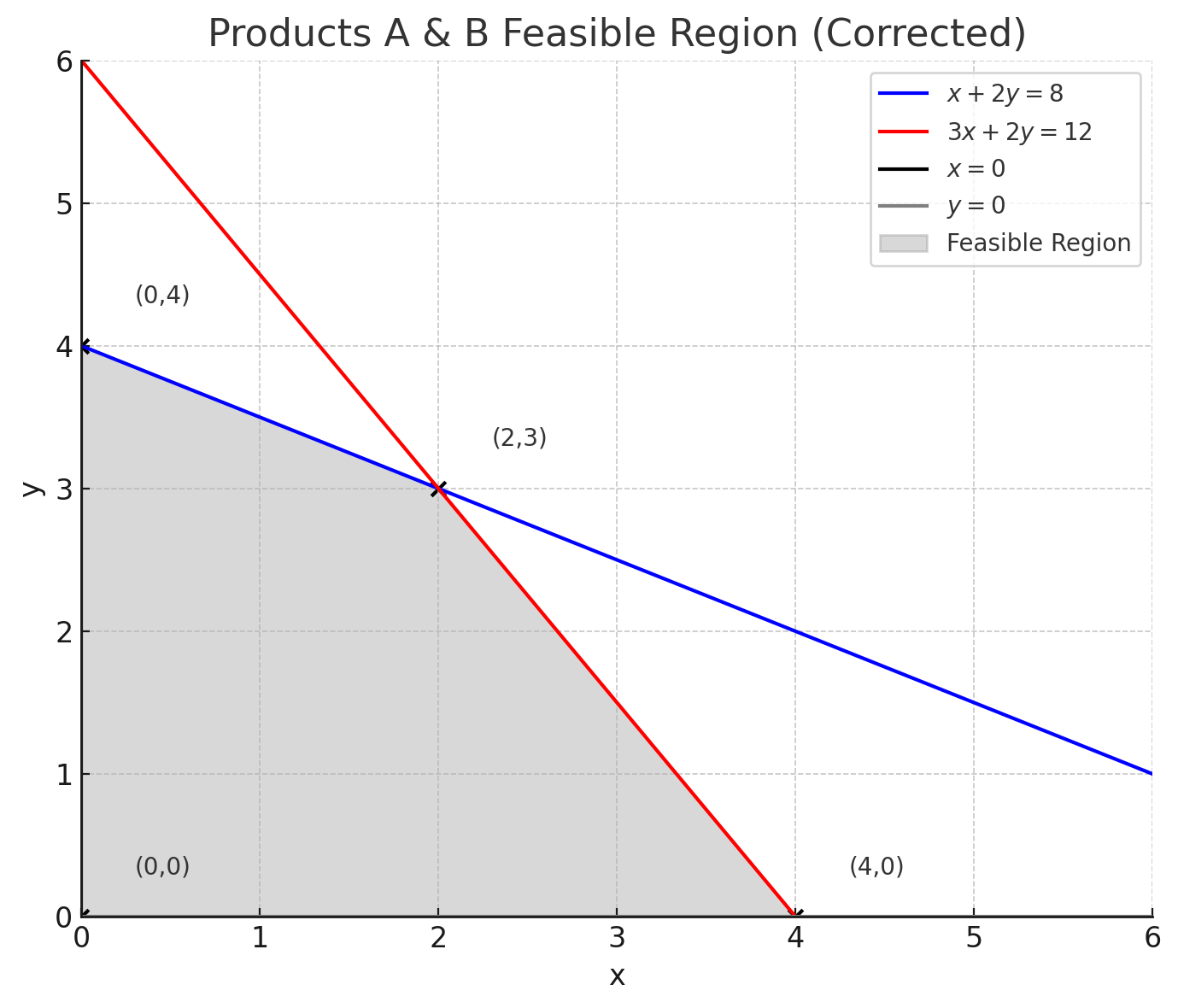
Step 5 – Corner points
(0,0), (4,0), (0,4)
Intersection of x + 2y = 8 and 3x + 2y = 12 → (2,3)
Step 6 – Evaluate objective function
P(0,0) = 0
P(4,0) = 80
P(0,4) = 120
P(2,3) = 130
Step 7 – Conclusion
Maximum profit = $130 at (x,y) = (2,3).
A company makes orange juice (x) and apple juice (y). Calculate the maximum profit given the below constraints:
Orange juice: 2 oranges + 1 hr per litre
Apple juice: 3 apples + 2 hrs per litre
Available: 40 oranges, 60 apples, 40 hours
Profit: $4 per orange juice, $5 per apple juice
Step 1 – Define variables
x = litres of orange juice
y = litres of apple juice
Step 2 – Objective function
Maximise:
P = 4x + 5y
Step 3 – Constraints
2x ≤ 40 → x ≤ 20 (oranges)
3y ≤ 60 → y ≤ 20 (apples)
x + 2y ≤ 40 (time)
x, y ≥ 0
Step 4 –Draw Graph
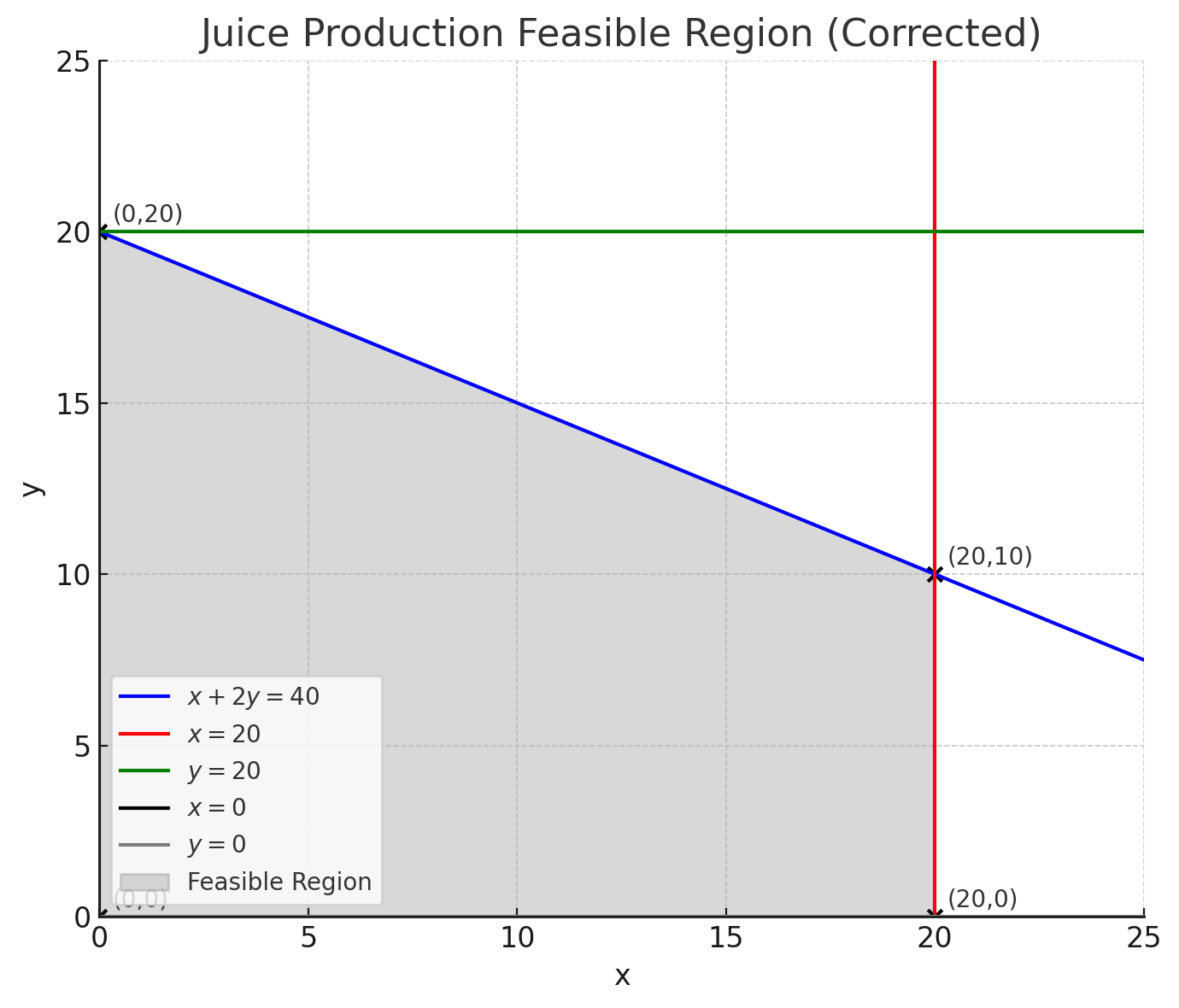
Step 5 – Corner points
(0,0), (20,0), (0,20), (20,10)
Step 6 – Evaluate objective function
P(0,0) = 0
P(20,0) = 80
P(0,20) = 100
P(20,10) = 130
Step 7 – Conclusion
Maximum profit = $130 at (x,y) = (20,10).
Summarise with AI:












GOOD PRESENTATION. DO YOU HAVE ONE ON COORDINATE GEOMETRY?
Thanks so much! I’m really glad you liked the presentation. Yes — we actually do have a great set of resources on coordinate geometry. You can find them here:
👉 https://www.superprof.co.uk/resources/academic/maths/geometry/
The language in the third question is confusing. “Offer A is a package of one shirt and a couple of pants which will sell for “. A couple of pants indicate 2 pants instead of a single pair of pant, it could’ve been renamed as a pair of pant. Couple of pant”s” means plural. Please change the language. From my understanding, the offer A consisted of 1 shirt and 2 pants, but in the solution, they have considered one shirt and one pant.
Thank you for your feedback! You’re absolutely right — the wording around “a couple of pants” was confusing. The problem has now been updated to clearly state that Offer A includes one shirt and one pair of pants, which aligns with the solution provided. We appreciate you taking the time to point this out and helping us improve the clarity of the question.
it can be nice when you help me to pass
Hi Matovu! Thank you for your comment! Wishing you best of luck with your studies!
Hi there, thanks for your comment and for taking the time to share your calculation!