Linear programming is a mathematical method used to find the maximum or minimum value of an objective function (like profit or cost) that depends on two or more decision variables, subject to certain constraints (like time, materials, or capacity).
A linear programming problem has three main parts:
- Decision variables — the unknowns to find.
- Objective function — what we want to maximise or minimise.
- Constraints — inequalities that limit the feasible region.
The solution is found graphically by plotting the inequalities, identifying the feasible region, and evaluating the objective function at its vertices (corner points).

Linear Programming Word Problem Example
A company produces two types of products: A and B. Each unit of A requires 2 hours of labour and 1 hour of machine time. Each unit of B requires 1 hour of labour and 2 hours of machine time. A total of 100 labour hours and 80 machine hours are available. Profit per unit is $40 for A and $50 for B. How many of each product should be produced to maximise profit?
Step 1 – Define the decision variables
x = number of product A units
y = number of product B units
Step 2 – Write the objective function
We want to maximise profit:
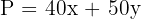
Step 3 – Write the constraints
Labour time:

Machine time:
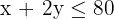
Non-negativity:
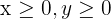
Step 4 – Graph the constraints
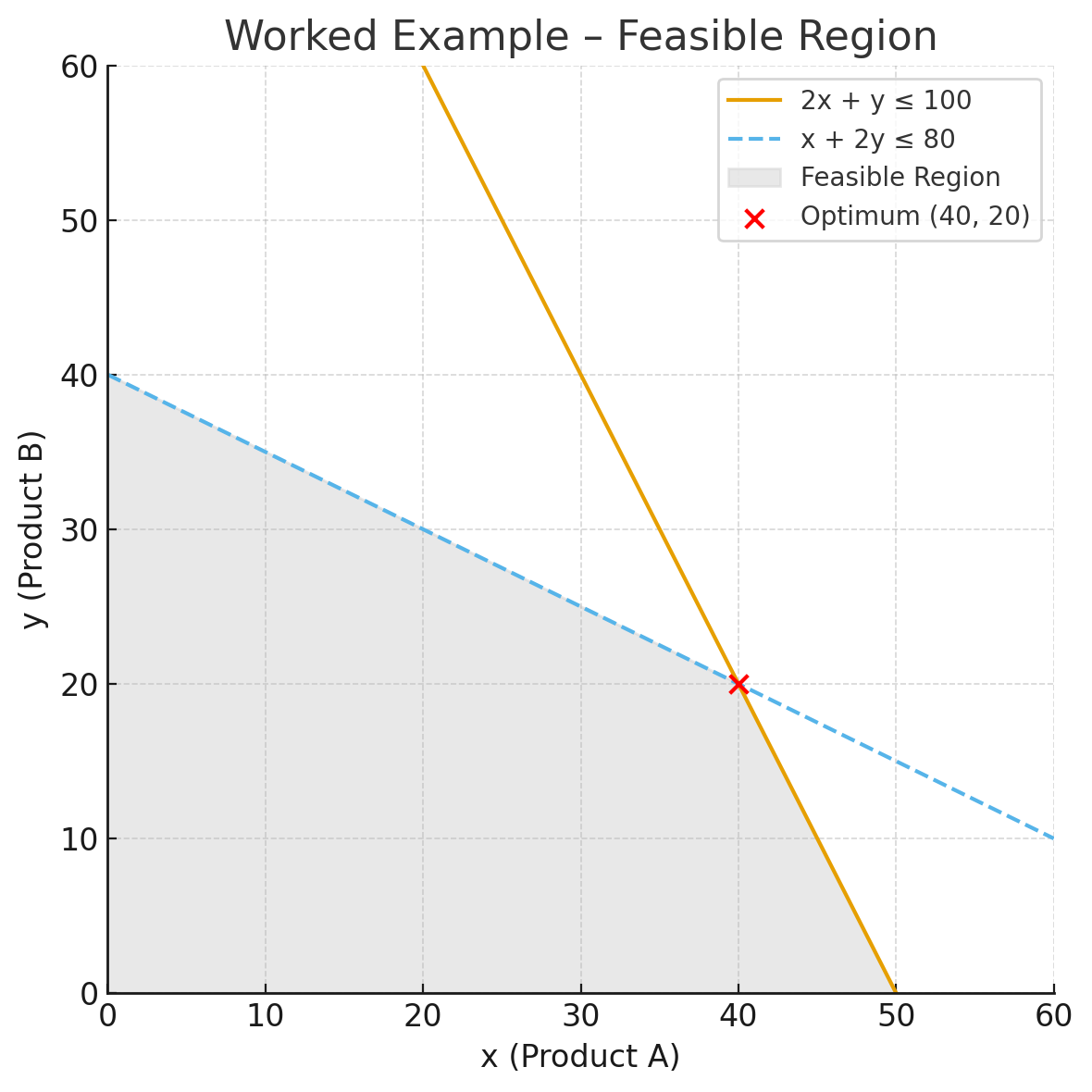
Step 5 – Find intersection points
Solve the system:
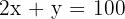
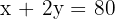
Multiply the second by 2 and subtract:
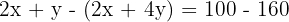
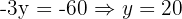
Substitute back:
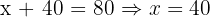
So the intersection point is (40, 20).
Step 6 – Evaluate profit at each vertex
Vertices: (0,0), (0,40), (40,20), (50,0)

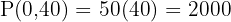
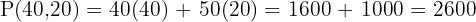
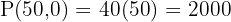
Step 7 – Choose the maximum
The maximum profit is $2600 at (40, 20).
Answer:
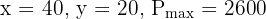
1. Define the decision variables
2. Write the objective function
3. Write the constraints
4. Graph the constraints
5. Find intersection points
6. Evaluate profit at each vertex
7. Choose the maximum
Permutation Practice Questions and Solutions
A factory produces chairs and tables.
Each chair requires 2 hours of carpentry and 1 hour of painting.
Each table requires 3 hours of carpentry and 2 hours of painting.
The factory has 60 hours of carpentry and 40 hours of painting available per week.
The profit per chair is $15 and per table is $20.
How many of each should be made to maximize profit?
Let:
x = chairs, y = tables
Objective function:
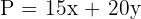
Constraints:
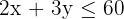
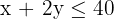

Intersection of 2x + 3y = 60 and x + 2y = 40:

Evaluate P at (0,0), (0,20), (30,0):


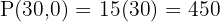
Answer:
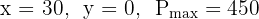
A farm grows wheat and corn.
Each hectare of wheat requires 3 labour days and 2 fertilizer units.
Each hectare of corn requires 2 labour days and 4 fertilizer units.
A total of 60 labour days and 80 fertilizer units are available.
Profit per hectare is $200 for wheat and $300 for corn.
Find how many hectares of each crop should be planted for maximum profit.
Let:
x= hectares of wheat, y = hectares of corn
Objective:

Constraints:
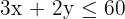


Find intersection:

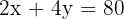
Multiply the first by 2 and subtract the second:

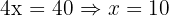
Substitute into 3x + 2y = 60:
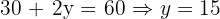
Vertices: (0,0), (0,20), (10,15), (20,0)
Evaluate:

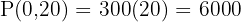
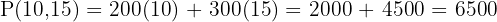
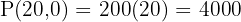
Answer:
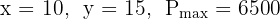
A nutritionist designs a diet using foods F1 and F2.
Each unit of F1 contains 3 units of protein and 1 unit of fat.
Each unit of F2 contains 1 unit of protein and 2 units of fat.
The diet must provide at least 6 units of protein and 4 units of fat.
The cost is $4 per unit of F1 and $3 per unit of F2.
Find the least costly diet.
Let:
x = F1 units, y = F2 units
Objective (minimize cost):
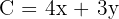
Constraints:
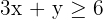


Solve for intersection:
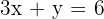
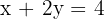
Multiply the second by 3 and subtract:
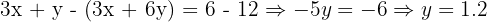
Substitute:
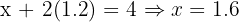
Evaluate cost at (1.6, 1.2):
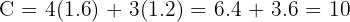
Answer:
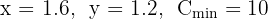












GOOD PRESENTATION. DO YOU HAVE ONE ON COORDINATE GEOMETRY?
Thanks so much! I’m really glad you liked the presentation. Yes — we actually do have a great set of resources on coordinate geometry. You can find them here:
👉 https://www.superprof.co.uk/resources/academic/maths/geometry/
The language in the third question is confusing. “Offer A is a package of one shirt and a couple of pants which will sell for “. A couple of pants indicate 2 pants instead of a single pair of pant, it could’ve been renamed as a pair of pant. Couple of pant”s” means plural. Please change the language. From my understanding, the offer A consisted of 1 shirt and 2 pants, but in the solution, they have considered one shirt and one pant.
Thank you for your feedback! You’re absolutely right — the wording around “a couple of pants” was confusing. The problem has now been updated to clearly state that Offer A includes one shirt and one pair of pants, which aligns with the solution provided. We appreciate you taking the time to point this out and helping us improve the clarity of the question.
it can be nice when you help me to pass
Hi Matovu! Thank you for your comment! Wishing you best of luck with your studies!
Hi there, thanks for your comment and for taking the time to share your calculation!