Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9

Exercise 1
Convert the following units into sexagesimal form:
8,179''
27,520''
Exercise 2
Convert the following units into decimal form:
12° 30' 42''.
Exercise 3
Express the following angles in degrees:
3 rad

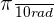
Exercise 4
Express the following angles in radians:
316°
10°
127º
Exercise 5
Calculate:
68º 35' 42'' + 56º 46' 39''.
Exercise 6
Calculate:
(132° 26' 33'') × 5
(128° 42' 36'') × 3
Exercise 7
Calculate:
(132° 26' 33'') : 3.
Exercise 8
Determine the complementary and supplementary angle of 38° 36' 43''.
Exercise 9
Determine the complementary and supplementary angle of 25° 38' 40''.
Solution of exercise 1
Convert the following units into sexagesimal form:
8,179''
The above number represents seconds and we have to convert it in the form of degree, minutes and seconds. To do so, first, we have to determine how many seconds are there in an hour.
1 hour = 3600 seconds
1 minute = 60 seconds
To convert seconds into degree, minutes and seconds, we will divide the seconds by 60 twice.

The quotient 136 will be further divided by 60 to get hours or degree like this:

The remainder will be minutes and the quotient is hour.
8179'' = 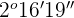
27,520''

The remainder 40 is seconds and the quotient 458 will be further divided by 60 to get hours or degree like this:
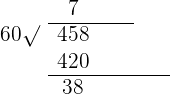
The remainder will be minutes and the quotient represents hour.
27520'' = 
Solution of exercise 2
Convert the following units into decimal form:
12° 30' 42''
2h = 2 x 3600s = 7200 s
48 min = 48 x 60 = 2880 s
30 s = 30 s
2 h 48 min 30 s = 10110s
Solution of exercise 3
Express the following angles in degrees:
3 rad
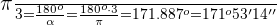

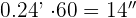

= 
= 
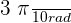
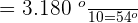
Solution of exercise 4
Express the following angles in radians:
316°

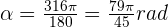
10°

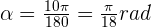
127º
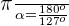
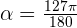
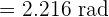
Solution of exercise 5
Calculate:
68º 35' 42'' + 56º 46' 39''.

Divide the seconds by 60, if they are greater than 60.
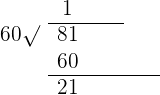
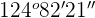
Repeat the same process for minutes
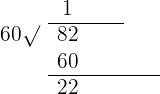
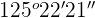
Solution of exercise 6
Calculate:
(132° 26' 33'') × 5
= 
Divide 165 by 60:

Add the quotient in minutes:
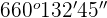
Divide 132 by 60:

Add 2 in hours:
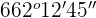
(128° 42' 36'') × 3
= 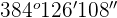
Divide 108 by 60 like this:
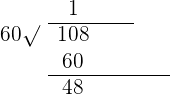
= 
Divide 127 by 60:
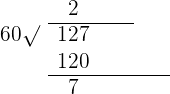
= 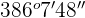
Solution of exercise 7
Calculate (132° 26' 33'') : 3
Divide hours by 3 like this:

The quotient 2 represents hours and the remainder 12 will be multiplied by 60 and the resulting number will be added to minutes:
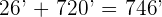
Repeat the same process for minutes:

The quotient 248 represents the minutes and the remainder 2 will be multiplied by 60 and the resulting number will be added to seconds:
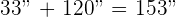
Hence, the final answer is:
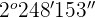
Solution of exercise 8
Determine the complementary and supplementary angle of 38° 36' 43''.
Complementary angle
We know that the sum of two supplementary angles is equal to 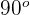 . So, we will subtract the above angle from
. So, we will subtract the above angle from 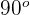 . Because the
. Because the 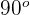 is not given in the form of minutes and seconds, so we will subtract 1 from
is not given in the form of minutes and seconds, so we will subtract 1 from 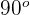 and place full degree 60' in minutes place. However, we do not have seconds either, so we will subtract 1 again from 60 to get 59'' and place it in the seconds place.
and place full degree 60' in minutes place. However, we do not have seconds either, so we will subtract 1 again from 60 to get 59'' and place it in the seconds place.
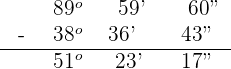
Supplementary angle
The sum of two supplementary angles is  . Hence, we will transform
. Hence, we will transform  to
to 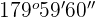 .
.

Solution of exercise 9
Determine the complementary and supplementary angle of 25° 38' 40''.
Complementary angle
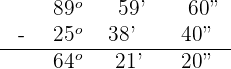
Hence, the complementary angle is 
Supplementary angle
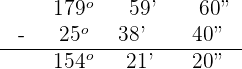
Hence, the supplementary angle is 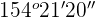 .
.













Time Is Amazing It’s More Than One