Chapters
In this article, we will discuss units of measuring angles and how to convert one unit into another.
There are three units to measure angles. These three units are revolutions, degrees, and radians which are discussed below in detail.

Revolutions
Revolution is one of the measure of angle. It forms when the initial side completes a full circle around its vertex until the side approaches its initial position. In other words, the initial and the terminal positions end up exactly in the same position. The revolution can be written as "rev". 1 revolution is equal to  .
.
Degrees
This is the most common way of measuring angles. In a single revolution, there are 360 degrees. We can divide the degrees further, for instance, one degree is equal to 60 minutes and one minute is equal to 60 seconds. Hence, the angle that measures one second is equal to 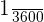 degrees. When we refer to the perpendicularity, we often mean an angle of 90 degree. We employ degrees to explain the triangles, like 15-75-90, 60-60-60, and 45-45-90. We write degrees with a tiny superscript circle at the top right side of a number. For instance, 90 degrees is written as
degrees. When we refer to the perpendicularity, we often mean an angle of 90 degree. We employ degrees to explain the triangles, like 15-75-90, 60-60-60, and 45-45-90. We write degrees with a tiny superscript circle at the top right side of a number. For instance, 90 degrees is written as 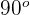 .
.
Radian
We define radian geometrically and we denote it by the symbol rad. Previously, radian was a SI supplementary unit, however now it is a SI derived unit. Mathematicians often use radians as it is based on the radius of the circle. The center of the circle is the vertex of the angle. One radian is equal to the 180 degree divided by  . We can write it mathematically as:
. We can write it mathematically as:
1 rad = 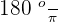
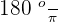 is approximately equal to 57.2958 degrees which is represented as:
is approximately equal to 57.2958 degrees which is represented as:
1 rad = 
In the next section, we will solve some examples in which we will convert one unit of angle to another.
Example 1
Convert  into radians.
into radians.
Solution
We have already discussed that one radian is equal to 180 degrees divided by  . So, we can write it mathematically as:
. So, we can write it mathematically as:
1 rad = 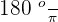
 is in the denominator on the right hand side of the equation, so we will move it to the left hand side and multiply it with radians like this:
is in the denominator on the right hand side of the equation, so we will move it to the left hand side and multiply it with radians like this:
 rad =
rad = 
Example 2
Convert 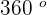 into radians.
into radians.
Solution
One radian is equal to 180 degrees divided by  . So, we can write it mathematically as:
. So, we can write it mathematically as:
1 rad = 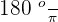
To isolate  on the right hand side of the equation, we will move
on the right hand side of the equation, we will move  on the left hand side like this:
on the left hand side like this:
 rad =
rad = 
We have to convert  into radians, so we will multiply the above equation by 2 like this:
into radians, so we will multiply the above equation by 2 like this:
 rad =
rad = 
 rad =
rad = 
Example 3
Convert 30 degrees into radians
Solution
One radian is equal to 180 degrees divided by  . So, we can write it mathematically as:
. So, we can write it mathematically as:
1 rad = 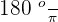
In this example, we don't have to convert 180 degrees to radians. Instead, we need to convert 30 degrees into radians. From the above formula, we can derive that  is equal to
is equal to  rad.
rad.
 =
=  rad
rad
Similarly, one degree is equal to  :
:

The angle  in radians is equal to the the angle
in radians is equal to the the angle  in degrees multiplied by
in degrees multiplied by  . Mathematically, we can write it as:
. Mathematically, we can write it as:
Radians = 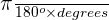
= 
= 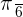 rad
rad
Hence, 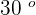 is equal to
is equal to 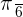 rad
rad
Example 4
Convert 2 rads into degrees.
Solution
One radian is equal to 180 degrees divided by  .
.
1 rad = 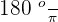
To determine the value of 2 radians, we will multiply the expression by 2:
2 rads = 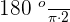
2 rads = 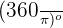
Example 5
Solution
 .
. 1 rad = 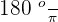
Hence,  is equal to
is equal to  rads. We can write it as:
rads. We can write it as:
 =
=  rads
rads
1 complete revolution is equal to 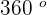 . Hence, 8 revolutions will be equal to:
. Hence, 8 revolutions will be equal to:
8 revolutions = 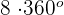
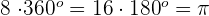 rads
rads
8 revolutions =  rads
rads
Example 6
Solution
 .
. 1 rad = 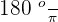
Hence,  is equal to
is equal to  rads. We can write it as:
rads. We can write it as:
 =
=  rads
rads
1 complete revolution is equal to 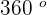 . Hence, 4 revolutions will be equal to:
. Hence, 4 revolutions will be equal to:
4 revolutions = 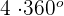
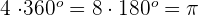 rads
rads
4 revolutions = 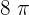 rads
rads
Example 7
Convert 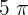 rads into degrees
rads into degrees
Solution
One radian is equal to 180 degrees divided by  .
.
1 rad = 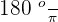
Hence,  is equal to
is equal to  rads. We can write it as:
rads. We can write it as:
 =
=  rads
rads
To find the  rads, we will multiply both sides of the equation with 5 like this:
rads, we will multiply both sides of the equation with 5 like this:
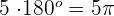 rads
rads
 rads
rads
Example 8
Convert  rads into degrees
rads into degrees
Solution
One radian is equal to 180 degrees divided by  .
.
1 rad = 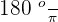
Hence,  is equal to
is equal to  rads. We can write it as:
rads. We can write it as:
 =
=  rads
rads
To find the  rads, we will multiply both sides of the equation with
rads, we will multiply both sides of the equation with  like this:
like this:
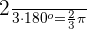 rads
rads
 rads
rads
Example 9
Convert 4 rads into degrees.
Solution
One radian is equal to 180 degrees divided by  .
.
1 rad = 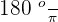
To determine the value of 4 radians, we will multiply the expression by 4:
4 rads = 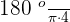
4 rads = 
Example 10
Solution
 .
. 1 rad = 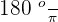
Hence,  is equal to
is equal to  rads. We can write it as:
rads. We can write it as:
 =
=  rads
rads
1 complete revolution is equal to 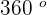 . Hence, 10 revolutions will be equal to:
. Hence, 10 revolutions will be equal to:
10 revolutions = 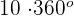
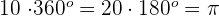 rads
rads
10 revolutions =  rads
rads
Example 11
Convert 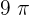 rads into degrees
rads into degrees
Solution
One radian is equal to 180 degrees divided by  .
.
1 rad = 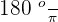
Hence,  is equal to
is equal to  rads. We can write it as:
rads. We can write it as:
 =
=  rads
rads
To find the 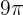 rads, we will multiply both sides of the equation with 9 like this:
rads, we will multiply both sides of the equation with 9 like this:
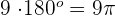 rads
rads
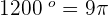 rads
rads
Example 12
Convert 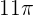 rads into degrees
rads into degrees
Solution
One radian is equal to 180 degrees divided by  .
.
1 rad = 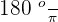
Hence,  is equal to
is equal to  rads. We can write it as:
rads. We can write it as:
 =
=  rads
rads
To find the 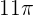 rads, we will multiply both sides of the equation with 11 like this:
rads, we will multiply both sides of the equation with 11 like this:
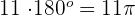 rads
rads
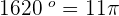 rads
rads













Time Is Amazing It’s More Than One