Chapters

Introduction
The sexagesimal number system also known as base 60 is a number system in which every unit is broken down (divided) into 60 smaller units. It is known as base 60 because we use 60 as a base. We use this system to measure time and angles.
In one hour, there are 60 minutes
In one minute, there are 60 seconds
1 h 
1º 
For example, 58 hours, 32 minutes and 45 seconds is written like this in the sexagesimal form:

Here, the degree represents hours, ' represents minutes, and '' depicts seconds.
Sumerians and Babylonians used this system, however, today, it is used to measure time and angles. We can convert the sexagesimal number into seconds and seconds into the sexagesimal form. In the next section, we will see how to make these conversions.
Converting Sexagesimal form into Decimals
1. Convert 3 hours, 36 minutes, 42 seconds to seconds.
In one hour, there are 60 minutes and in one minute, there are 60 seconds. Hence, we will write these units like this to attain a decimal form:
3h = 3 x 3600 s = 10, 800 s
36 min = 36 x 60 s = 2160 s
42 s = 42
3 hours 36 min 42 seconds = 13,002 seconds
2. Convert 5 hours, 16 minutes, 29 seconds to seconds.
In one hour, there are 60 minutes and in one minute, there are 60 seconds. Hence, we will write these units like this to attain a decimal form:
5h = 5 x 3600 s = 18,000 s
16 min = 16 x 60 s = 960 s
29 s = 29 s
5 hours 16 min 29 seconds = 18,989 seconds
Converting Decimals into Sexagesimal Form
To convert the smaller units into the larger units, we divide. Consider the following examples
1 Convert 7520'' into degree, minutes and seconds
We know that in one hour there are 60 minutes and in one minute there are 60 seconds. Hence, in one hour, there are 3600 (60 x 60) seconds. To get the hours we will use the division operation twice.
Step 1
First, we will divide 7250 by 60 to get seconds like this

Step 2
The remainder 20 represents seconds and the quotient 125 will be divided by 60 further to get hours and minutes:
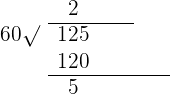
The remainder 5 represents minutes and the quotient 2 reflects hours. Hence, the final answer is:

2 Convert 12,900'' into degree, minutes and seconds
We know that in one hour there are 60 minutes and in one minute there are 60 seconds. Hence, in one hour, there are 3600 (60 x 60) seconds. To get the hours and minutes, we will use the division operation twice.
Step 1
First, we will divide 12,900 by 60 like this:
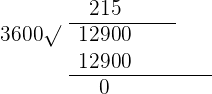
Step 2
The remainder zero represents the seconds and the quotient 215 will be further divided by 60 to get minutes and hours like this:

The remainder 35 represents the minutes and the quotient 3 reflects hours. We will write the final answer like this:
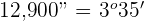
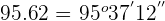
2 Convert 48.27 in degree minute and seconds
48 is a degree because it is the whole number part. Let us find minutes and seconds.
0.27 x 60 = 16.2
Again, the whole number part 16 will be considered as minutes. Now, we will multiply 0.2 with 60 to get seconds.
0.2 x 60 = 12 seconds
Hence, we will write the decimal number 48.27 in degree, minutes and seconds like this:

3 Convert 82.27 in degree minute and seconds
82 is a degree because it is the whole number part. Let us find minutes and seconds.
0.27 x 60 = 16.2
Again, the whole number part 16 will be considered as minutes. Now, we will multiply 0.2 with 60 to get seconds.
0.2 x 60 = 12 seconds
Hence, we will write the decimal number 95.62 in degree, minutes and seconds like this:

Operations with Sexagesimal Numbers
We can add, subtract, multiply and divide numbers in sexagesimal form. We will discuss each operation below one by one with the examples.
Addition
Add 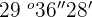 and
and 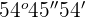 .
.
Follow these steps to add the above two numbers.
Step 1
Add the numbers by putting hours under hours, minutes under minutes and seconds under seconds like this:

Step 2
If the seconds are greater than 60, then divide the number by 60 and add the quotient to minutes like this:
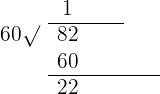
The remainder 22 is seconds and the quotient will be added to the minutes. Hence, the new number is 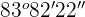 .
.
Step 3
Repeat the same procedure for the minutes.
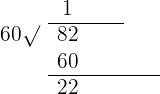
The new number is 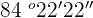 .
.
Subtraction
Subtract 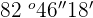 and
and  .
.
Follow these steps to subtract the above two numbers.
Step 1
Subtract the numbers by putting hours under hours, minutes under minutes and seconds under seconds like this:

Step 2
If the number in the second column is less than 0, then add 60 in the seconds and subtract 1 from minutes of the upper number like this:
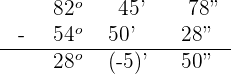
Step 3
Repeat the same process for the minutes.
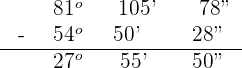
Hence, the final number is 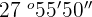 .
.
Multiplication
Multiply 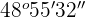 by 6.
by 6.
Follow these steps to complete the multiplication.
Step 1
Multiply each part one by one by 6.
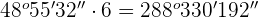
Step 2
If the second part is greater than 60, then divide it by 60 and add the quotient to the minutes and the remainder will be the seconds.

The new number is 
Step 3
Repeat the same procedure for minutes.

The new number is 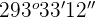
Division
Divide the numbers 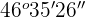 by 5.
by 5.
Follow these steps to divide the numbers.
Step 1
Divide the hours by the number like this:

The remainder is 1 and the quotient is 9. The quotient 9 represents the hours and we will multiply the remainder by 60 and add it to minutes.
35' + 60' =95'
Step 2
Repeat the same procedure for minutes.
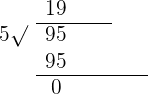
The quotient 19 is the minutes and the remainder 0 will be multiplied by 60 and the resulting number will be added to seconds.
26'' + 0'' = 26''
Step 3
Repeat the same procedure for seconds
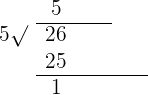
Hence, the final number is  .
.













Time Is Amazing It’s More Than One