Chapters
Dividing integers is easier than the rest of the mathematical operations. If you learned all the other mathematical operations then you won't have any trouble with this one. At this point, you must have realized how important the signs are for integers. These signs matter a lot because later on when you will be studying more advanced mathematics, you will encounter a lot of problems which include changes in signs. For example, you are finding the direction of a boat where the wind is moving West at some velocity. The direction of your answer will matter a lot, let's say you did some miss calculation and got an answer as negative which indicates a specific direction, let's say East. You checked your calculations and saw that you accidentally added a minus sign with the answer, now you corrected it and the answer becomes positive which means that the direction is now West. Did you see how a sign changed the whole course of the boat? This was a very small example, even big companies like NASA, SpaceX, etc. uses integers to do their calculations for the projectile motion of their rockets now think if they made an error in signs, what will it cost?
Dividing integers has two parts. The first part is to divide the absolute values that is pretty simple. The next part is to add the resultant sign to the resultant absolute value. To find the resultant sign, you need to remember two points which are:
- If both integers have the same signs that mean the resultant absolute value will have a positive sign.
- If both integers have different signs that mean the resultant absolute value will have a negative sign.


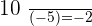
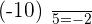

Properties
Like every mathematical operation, division of integers also has some properties. Below are all the properties:
Property No.1: Doesn't Follow Closure Property
This property tells that if you divide two integers this will result in a new number which will not always be an integer.
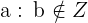
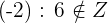
Property No.2: It is not Commutative
When you are dividing two integers, the order does change the division.
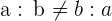
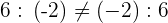

Summarise with AI:













Integer word problems with answers
Goooooooood exercises
Awesome👏👍😊
hey tamilu
The questions were good even though I was confused with the 5th one
Questions are Awesome..
I like it!