Like other mathematical operations, you can also multiply integers with integers. Although the multiplication is the same there is a small twist which we will discuss later. When you multiply any integer with another integer (both integers can be of any type), the absolute value of the product is the multiplication of the absolute values of the factors. In simple words, you will be multiplying both numbers but what is the twist then? It is the sign. Integers are well known for their sign complex. Since they exist in positive as well as negative, applying any kind of mathematical operation will become difficult and there is no exception for multiplication. When you multiply two integers, their signs also multiply. In conclusion, the absolute values not only multiples but the sign of the product can be determined by using the rule of signs.

Sign Multiplication
When you are multiplying integers, you should remember that their signs also multiplies. You must have heard numbers multiplying but sign multiplying? Yes, this is a very important step. In fact, later when you will be doing advanced mathematics questions, you will encounter sign multiplications very frequently. Sign multiplication isn't hard, all you need to know are two rules and then you can easily multiply signs. Below are the two rules:
- If two integers have the same signs then the resultant absolute value will be a positive integer.
- If two integers have different signs then the resultant absolute value will be a negative integer.
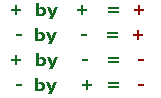
Below are some examples that will help you to understand it better.
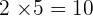
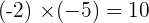

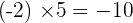
Properties of the Multiplication of Integers
There are some properties of multiplication of integers that will help you to encounter different mathematical problems which include integers. Below are all the properties.
Property No.1: Closure
This property tells that if you add two integers this will result in a new number which will also be an integer.
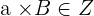
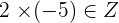
Property No.2: Associative
It doesn't matter what way you group, it will always result in the same. In simple words, the way in which the multiples are grouped does not change the result.
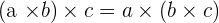
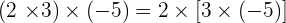
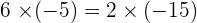
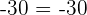
Property No.3: Commutative
When you are multiplying two integers, the order doesn't change the sum.

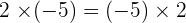

Property No.4: Multiplicative Identity
Multiplying one will not change the overall result because one is a natural element. If you multiply one to any number, it will always give the same number.
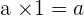

Property No.5: Distributive
The product of a number for a sum is equal to the sum of the products of this number for each of the addends.
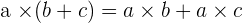
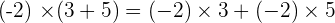
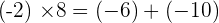
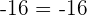
Removing a common factor:
It is the reverse of the distributive property.
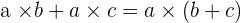
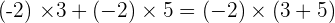
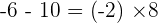
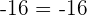
Summarise with AI:













Integer word problems with answers
Goooooooood exercises
Awesome👏👍😊
hey tamilu
The questions were good even though I was confused with the 5th one
Questions are Awesome..
I like it!