Chapters
In this article, you will learn what are integers, how to subtract them, and what are the properties of subtraction of integers. But before discussing the integers, we will see what are different types of numbers.

Types of Numbers
Many different types of numbers exist. Some are explained below.
Natural Numbers
These numbers are also known as counting numbers and are always positive. They start from 1 and go forward to infinity. They are expressed as:
1, 2, 3, 4, 5, 6, 7, 8, 9, .......
Whole Numbers
Whole numbers start from 0, unlike natural numbers that start from 1. They include 0 and all the natural numbers after 0. They are expressed as:
0, 1, 2, 3, 4, 5, 6, .....
Integers
These numbers include zero, all positive natural numbers, and negatives of natural numbers. They extend to infinity on both sides of the number line because there is no definite starting or ending point of these numbers. They are expressed as:
...., -5, -4, -3, -2, -1 , 0, 1, 2, 3, 4, .....
Rational Numbers
Rational numbers exist as fractions or ratios of integers. In other words, we can say that the rational numbers can be expressed in the form of 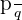 , where
, where 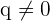 . The examples of rational numbers include
. The examples of rational numbers include  ,
, 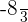 , and
, and 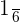 .
.
Have you noticed that each number type contains a previous type within it?
The whole numbers are natural numbers but include zero. The integers are whole numbers, but also include the negatives of natural numbers. The rational numbers are integers, but with division operation. Remember that you can make an integer a rational number by just putting one in the denominator. For instance, the integer -9 can also be written in the form of a fraction  . Both -9 and 1 are integers, so -9 is also a rational number.
. Both -9 and 1 are integers, so -9 is also a rational number.
Irrational Numbers
Now, the question arises what are those numbers called that cannot be expressed as fractions? Well, such numbers fall in another major category of numbers, irrational numbers. The fractions are also referred to as rational numbers and they can be expressed as terminating or repeating decimals. For instance, 1.5 can be written as 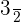 and 0.4 is equal to
and 0.4 is equal to 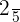 .
.
We have the numbers that are non-repeating and non-terminating decimals. These numbers are irrational because we cannot convert them into fractions. For instance, the number 4.3456721.... cannot be expressed as a fraction because the numbers after the decimal point are non-terminating and non-repeating. Hence, this is an irrational number. Rational and irrational numbers are two distinct number types and they never overlap.
Real Numbers
When we combine the set of rational and irrational numbers, we get a new set, known as a real number. Besides complex numbers which can be written as 5 - 7i, every number is a real number. In other words, unless a number has i in it, it is a real number.
So, what can be deduced from the above discussion?
The answer is simple. Every rational or irrational number is also a real number, but every real number may not necessarily be a rational or irrational number.
We will answer some of the common questions regarding integers below.
Is an integer also a rational number?
Yes, every integer is also a rational number because we can convert an integer into a fraction by putting 1 in the denominator.
Is a rational number also an integer?
Not always. For example, the rational number 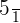 is also an integer because it is equal to 5. However, the rational number
is also an integer because it is equal to 5. However, the rational number 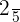 is not an integer.
is not an integer.
Now, that we know what are integers and how they differ or are related to other types of numbers, let us proceed to discuss how to subtract integers.
Subtracting Integers
Follow these steps to subtract integers:
Step 1 - Keep the first number as it is.
Step 2 - Change the operation of the second number from positive to negative or if the second number already has a minus sign, then make it positive.
Step 3 - After getting the opposite sign of the second number, but that number and its sign in parenthesis and place a positive sign between numbers.
Step 4 - Proceed with the regular addition of numbers.
Let us solve some examples.
Example 1
Solve 8 - 3
Solution
= 8 + (-3)
= 5
Example 2
Solve 9 - 11
Solution
= 9 + (-11)
= -2
Properties of Subtraction of Integers
Now, we will discuss some properties of subtraction of integers.
Closure Property
The closure property of subtraction of integers says that the difference of two integers will result in another integer. For instance, if a and b are two integers, then their difference will result in a new number which will be also an integer. Mathematically, we can express the closure property of subtraction like this:
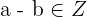
Remember that we use the symbol Z to express integers
Consider the following example.
Prove that 9 - 7 is an integer.
= 9 + (-7)
= 2
After subtracting 7 from 9, we got the number 2 which is an integer.
Distributive Property
The distributive property of subtraction of integers says that we can distribute the ability of operation over another arithmetic operation within parentheses. In the case of subtraction, we call this property the distributive property of multiplication over subtraction. In this case, we subtract the integers first and then multiply or we can also multiply first with each number within the parenthesis and take the difference later.
Suppose a, b and c are three integers. The distributive property of multiplication over subtraction can be expressed as:
a x (b - c) = ab - ac
Or
a x (b - c) = a x b - a x c
Let us use this property to solve the following examples:
1. Using the distributive property of subtraction of integers prove 10 x (5 - 6) = 10 x 5 - 10 x 6.
10 x (5 - 6) = 10 x 5 - 10 x 6
10 x (-1) = 50 - 60
-10 = -10
2. Using the distributive property of subtraction of integers prove -2 x (2 - 3) = -2 x 2 - (-2) x 3
-2 x (2 - 3) = -2 x 2 - (-2) x 3
- 2 x ( -1) = -4 + 6
2 = 2
The other properties of integers are commutative and associative. These properties are true for addition and multiplication, but not for subtraction. Why these properties do not hold true for subtraction is explained below.
Commutative Property of Addition and Multiplication
The commutative property of addition and multiplication says that the order of integers is not important. However, for subtraction, the order of numbers does matter. For addition and multiplication, the commutative property is mathematically represented like this:
a + b = b + a
a x b = b x a
However, if we change the order of integers for subtraction, the left and right hand sides will not be the same. Mathematically, we can write it as:
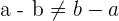
Consider the following example:
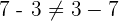
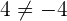
Associative Property of Addition and Multiplication
The associative property of addition and multiplication says that the way of the grouping of integers doesn't matter because both the left and right-hand sides will be equal. For instance, if there are three numbers a, b, and c, then this property can be mathematically represented like this:
(a + b) + c = a + (b + c)
(a x b) x c = a x (b x c)
This property if untrue for subtraction, so we can mathematically express it as:
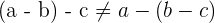
Consider the following example:

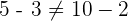

Summarise with AI:













Integer word problems with answers
Goooooooood exercises
Awesome👏👍😊
hey tamilu
The questions were good even though I was confused with the 5th one
Questions are Awesome..
I like it!