
if you are dealt with 3 cards, what is the probability of being delt all queens ?
use probability with combinations to solve the problem
Answers
Assuming the deck is entirely random, then the probability of getting 3 queens is given by:
This comes from the following, in order of the calculation:
When we start dealing we have 52 cards, of which four are queens. We want any one of the four queens to be our first card. Assume that any card is equally likely to be dealt. Then there are 52 distinct cards that we can be given, and 4 of them are queens, so the probability of getting a queen is 4/52 = 1/13.
Proceed to the second card. Now we have only 3 queens left, and also only 51 cards left. Using the same reasoning above, the probability of getting a queen is 3/51 = (13)/(173) = 1/17.
On the third and final card we are interested in, now there are only two queens left and 50 cards in total - so we get P(queen dealt) = 2/50 = 1/25.
Why multiply? Because each of the third and second cards being queens is only relevant if the first card was a quen, and then if the second cards was also a queen. This means that the overall probability is the product of all other probabilities.
Finally, since there are 4 queens and we want any three of them, the suit of the queen does not matter to an individual probability, but does increase the number of ways we can get free queens. Called the Queen of Hearts H, etc., and (C = clubs, D = diamonds, S = Spades), these are the ways of getting 3 queens, assuming that the order does not matter (which it doesn't here):
CHD CHS CDS DHS
i.e. 4 distinct ways of getting 3 queens out of the deck. So we multiply our earlier calculation by 4. This can be written 4C3 where 4 is the number of queens available to choose from, and we choose 3. (Usually the 4 is written to the top left of the C, and the 3 to the bottom-right, but I don't know how to format this properly.) You should be told how to calculate this in classes, but it's written:
with:
and so on
Hope this helps.
07 November 2012

Add an answer
Similar questions
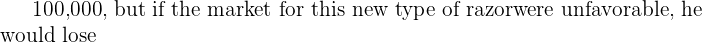 60,000. Since Ron Bush is a good friend of Jim Sellers, Jim is considering the possibility of using Bush Marketing Research to gather additional information about the market for the razor. Ron has suggested that Jimeither use a survey or a pilot study to test the market. The survey would be a sophisticated questionnaire administered to a test market. It will cost
60,000. Since Ron Bush is a good friend of Jim Sellers, Jim is considering the possibility of using Bush Marketing Research to gather additional information about the market for the razor. Ron has suggested that Jimeither use a survey or a pilot study to test the market. The survey would be a sophisticated questionnaire administered to a test market. It will cost  20,000. Ron Bush has suggested that it would be a good idea for Jim to conduct either the survey or the pilot before Jim makes the decision concerning whether to produce the new razor. ButJim is not sure if the value of the survey or the pilot is worththe cost. Jim estimates that the probability of a successful market without performing a survey or pilot study is0.5. Furthermore, the probability of a favorable survey result given a favorable market for razors is 0.7, and the probability of a favorable survey result given an unsuccessful market for razors is 0.2. In addition, the probability of an unfavorable pilot study given an unfavorable market is 0.9, and the probability of ann unsuccessful pilot study result given a favorable market for razors is 0.2.
20,000. Ron Bush has suggested that it would be a good idea for Jim to conduct either the survey or the pilot before Jim makes the decision concerning whether to produce the new razor. ButJim is not sure if the value of the survey or the pilot is worththe cost. Jim estimates that the probability of a successful market without performing a survey or pilot study is0.5. Furthermore, the probability of a favorable survey result given a favorable market for razors is 0.7, and the probability of a favorable survey result given an unsuccessful market for razors is 0.2. In addition, the probability of an unfavorable pilot study given an unfavorable market is 0.9, and the probability of ann unsuccessful pilot study result given a favorable market for razors is 0.2.