
Probability
There are 130 black and red balls in a pot. If 30 are black, how many black balls will you need to add to the box to increase picking a black to 0,5?
Answers
There are 130 black and red balls in a pot. If 30 are black, how many black balls will you need to add to the box to increase the probability of picking a black to 0,5?
17 April 2019
So if the total number i.e. 1 is = 130, then to have a value of 0.5, half of 1, you need to half 130 balls. This is 65. Therefore for there to be 0.5 probability of picking black, there must in total be 65 black balls. We already have 30 balls, so how many more do we need to get to 65?65-30 = 35. You need to add 35 more black balls.
18 April 2019
The probability of 0.5 is a half, this means 1/2 of the balls must be black. In order to figure this out we need to know how many red balls there are, so this means we subtract 30 (number of black balls) from 130 (total amount) . The awnser is 100 (amount of red balls) since we need black and red balls to be the same amount we will need to take 30 away from 100 to find out how many more black balls will make it equal. So since 100-30 = 70. You will need to add 70.
21 April 2019
Required probability=0.5as 30 balls are black so probability= 30/130 now it increase it to 0.5 to add x black ballso(30+x)/130=0.530+x=130*0.530+x=65x=35so we would add 35 black ball to getting probability 0.5
23 April 2019
we need to add 35 black balls to increase probability of picking black ball to 0.5
25 April 2019
Jessicahannah is the only person who is replied correctly.The mistake others were making is forgetting that when adding black balls, we increase the total number of balls. It always helps if you simplify the numbers in a problem. Imagine we were told that there were 8 black and red balls, and 3 were black. How many black balls would we need to add? At the moment, we have 3/8. So if we add one we will have half? 4/8? No, we will have 4/9. So we must first work out how many red balls there are: 8 - 3 = 5. Now we can add 2 black balls to our 3 original balls, so we have 5. Now there are 10 balls total, 5/5. Jessicahannah demonstrates this method well with the original question.
08 May 2019
increasing the probability of picking back to 0,5 means it wil be as likely you pick black as you pick red. So there needs to be an equal chance of picking red or black, in this case, To achieve this, you will need to add 70 black balls to the 30 in the pot, to match the 100 red balls already in the pot.
19 May 2019
130 are total balls out of which 30 are black and 100 are red, so if you need to get 0.5 probability black balls should be equal to red balls ie 70 more black balls are needed to get probability of 0.5
20 May 2019
To increase the probability to 0.5 there should be equal no. of balls of both black and red colour. As of now there are 30 black Balls out of 130 ,that means 130-30=100 red balls are there in pot. To for 0.5 probability black Balls also have to 100. As 30 balls are already there so we have to put 100-30=70 balls in pot
28 July 2019
35. 0.5 off the balls is 65. 65 minus 30 is 35.
05 December 2019
P(black) = 0.5 = x/130x = 65 black balls total65 - 30 = 35 more needed
23 January 2020
At the moment we have 130 balls. If 30 are black then 100 are red.For the probability of picking a black=0.5 half the balls must be black. this can be expressed as (Number of black balls)/(Total number of balls)=0.5So we need an equal number of black and red balls. We have 100 red balls so we need 70 more black balls. Then we will have 100 red and 100 black balls.
23 March 2020

Add an answer
Similar questions
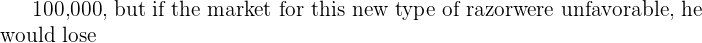 60,000. Since Ron Bush is a good friend of Jim Sellers, Jim is considering the possibility of using Bush Marketing Research to gather additional information about the market for the razor. Ron has suggested that Jimeither use a survey or a pilot study to test the market. The survey would be a sophisticated questionnaire administered to a test market. It will cost
60,000. Since Ron Bush is a good friend of Jim Sellers, Jim is considering the possibility of using Bush Marketing Research to gather additional information about the market for the razor. Ron has suggested that Jimeither use a survey or a pilot study to test the market. The survey would be a sophisticated questionnaire administered to a test market. It will cost  20,000. Ron Bush has suggested that it would be a good idea for Jim to conduct either the survey or the pilot before Jim makes the decision concerning whether to produce the new razor. ButJim is not sure if the value of the survey or the pilot is worththe cost. Jim estimates that the probability of a successful market without performing a survey or pilot study is0.5. Furthermore, the probability of a favorable survey result given a favorable market for razors is 0.7, and the probability of a favorable survey result given an unsuccessful market for razors is 0.2. In addition, the probability of an unfavorable pilot study given an unfavorable market is 0.9, and the probability of ann unsuccessful pilot study result given a favorable market for razors is 0.2.
20,000. Ron Bush has suggested that it would be a good idea for Jim to conduct either the survey or the pilot before Jim makes the decision concerning whether to produce the new razor. ButJim is not sure if the value of the survey or the pilot is worththe cost. Jim estimates that the probability of a successful market without performing a survey or pilot study is0.5. Furthermore, the probability of a favorable survey result given a favorable market for razors is 0.7, and the probability of a favorable survey result given an unsuccessful market for razors is 0.2. In addition, the probability of an unfavorable pilot study given an unfavorable market is 0.9, and the probability of ann unsuccessful pilot study result given a favorable market for razors is 0.2.