
probability
There are 4 blue counters and 8 yellow counters in a bag. What is the probability of choosing a blue counter, not replacing it, then choosing a yellow counter?
Answers
How this works is when a variance of probability isn't replaced then it reduces total fractional amount as a probability.So the first trial would be 4/12=blue (12 because the total units involved is 12)This can be simplified as 1/3 one thirdSince is it not replaced then the total amount will decrease as well as the variant deducted.So the second trial would be 8/11=yellowStrangely enough this increases the probability of the yellow because there are less variables.To complete the process you need to connect these two trials together, this is where you would multiply.4/12 x 8/11 = 32/132 you would simplify this by dividing by the highest that can go into the numerator and the denominator which is 4 = 8/33 this would be your final answer.
03 April 2019
One of the easiest ways to find this is by drawing a probability tree diagram. There would be two different branches: the first branch being the first ball picked out, and the second would be the second ball picked out without the first being replaced. The probability of picking out a blue counter the first time would be 4/12 since there are 12 counters in total and 4 of them are blue. 8/12 would be the probability of picking a yellow counter since there are 8 yellow counters. Then we move onto the second branch after we have already picked a blue counter. Since we have not replaced the first counter, there are now 11 counters in the bag, 3 of which are blue since one was already taken out, and 8 of which are yellow from before. This means the probability of a yellow counter in the second pick is 8/11. We now multiply both the probabilities, the probability of a blue counter the first time and a yellow counter in the second pick which would be 4/12 x 8/11 = 32/132. This can then be simplified by dividing both the numerator and denominator by 4 giving us 8/33.
29 April 2019
Probability of choosing a blue counter = 4/(4+8)=4/12=1/3Not replacing the blue counter then the probability of choosing an yellow counter = 8/(8+3)=8/11
22 May 2019

Add an answer
Similar questions
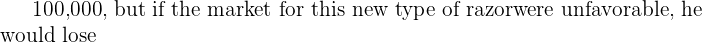 60,000. Since Ron Bush is a good friend of Jim Sellers, Jim is considering the possibility of using Bush Marketing Research to gather additional information about the market for the razor. Ron has suggested that Jimeither use a survey or a pilot study to test the market. The survey would be a sophisticated questionnaire administered to a test market. It will cost
60,000. Since Ron Bush is a good friend of Jim Sellers, Jim is considering the possibility of using Bush Marketing Research to gather additional information about the market for the razor. Ron has suggested that Jimeither use a survey or a pilot study to test the market. The survey would be a sophisticated questionnaire administered to a test market. It will cost  20,000. Ron Bush has suggested that it would be a good idea for Jim to conduct either the survey or the pilot before Jim makes the decision concerning whether to produce the new razor. ButJim is not sure if the value of the survey or the pilot is worththe cost. Jim estimates that the probability of a successful market without performing a survey or pilot study is0.5. Furthermore, the probability of a favorable survey result given a favorable market for razors is 0.7, and the probability of a favorable survey result given an unsuccessful market for razors is 0.2. In addition, the probability of an unfavorable pilot study given an unfavorable market is 0.9, and the probability of ann unsuccessful pilot study result given a favorable market for razors is 0.2.
20,000. Ron Bush has suggested that it would be a good idea for Jim to conduct either the survey or the pilot before Jim makes the decision concerning whether to produce the new razor. ButJim is not sure if the value of the survey or the pilot is worththe cost. Jim estimates that the probability of a successful market without performing a survey or pilot study is0.5. Furthermore, the probability of a favorable survey result given a favorable market for razors is 0.7, and the probability of a favorable survey result given an unsuccessful market for razors is 0.2. In addition, the probability of an unfavorable pilot study given an unfavorable market is 0.9, and the probability of ann unsuccessful pilot study result given a favorable market for razors is 0.2.