Chapters
In mathematics, the concepts of mean proportional, third proportional, and fourth proportional are all rooted in the idea of ratios and proportions. These concepts extend the basic knowledge of proportional relationships taught at GCSE level, and they are foundational to more advanced problem-solving encountered in A-Level Maths, especially in algebra and geometry.
These proportionals involve setting up equal ratios and solving for unknown values. Although they may sound complex at first, they follow predictable patterns and formulas that become intuitive with practice.
📘 What is a Proportion?
A proportion is a statement that two ratios are equal. For example:
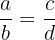
This relationship implies that the quantity a is to b as c is to d. The terms "extremes" and "means" are used in this context:
Means: The middle two terms (b and c)
Extremes: The first and last terms (a and d)
📌 Mean Proportional (Geometric Mean)
The mean proportional between two positive numbers, a and b, is the number x that satisfies the proportion:
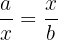
Solving for x:
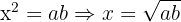
This is also known as the geometric mean of a and b. It appears in both GCSE (particularly in higher-tier problems involving ratio and geometry) and A-Level mathematics, where it’s used in topics like geometric sequences, similarity, and coordinate geometry.
📌 Third Proportional Formula
Given two numbers a and b, the third proportional is a number x such that:
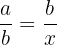
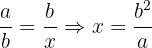
This concept is a specific application of equal ratios, the underlying algebra appears frequently when working with ratios, scaling, or indirect proportion.
📌 Fourth Proportional Formula
If you are given three numbers—a, b, and c—the fourth proportional is a number x such that:
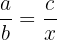
Solving for x:
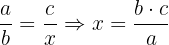
This type of proportional reasoning is foundational in problems involving compound ratios and appears in GCSE Higher Tier, as well as in early A-Level topics like function scaling, coordinate geometry, and algebraic manipulation.
In the next section, we will solve some examples in which we will calculate third, fourth and mean proportional.
📝 Mean Proportional Problems and Worked Solutions
Find the fourth proportional to 3, 5 and 6.
Suppose the fourth proportional is x. We can write the above numbers in proportional form like this:
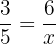
Take x on the left hand side of the equation and the fraction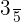 
on the right hand side.
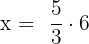
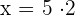
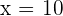
Hence, the fourth proportional is 10.
Find the fourth proportional to 11, 15 and 22.
Suppose the fourth proportional is x. We can write the above numbers in proportional form like this:
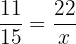
Take x on the left hand side of the equation and the fraction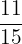 
on the right hand side.
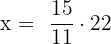
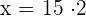
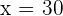
Hence, the fourth proportional is 30.
Find the fourth proportional to x + 3x, x + 2 and 5x, if x = 3.
In this example, first, we will calculate the quantities by substituting x = 3.
First quantity = 3 + 3(3) = 12
Second quantity = x + 2 = 5
Third quantity = 5x = 5 (3) = 15
Suppose the fourth proportional is x. We can write the above numbers in proportional form like this:
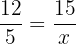
Take x on the left hand side of the equation and the fraction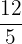 
on the right hand side.
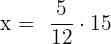
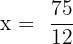
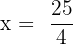
Hence, the fourth proportional is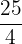 
.
Find the third proportional to 2, 9 and 15.
Suppose the third proportional is x. We can write the above numbers in proportional form like this:
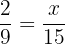
Multiply both sides by 15 to isolate x on the either side of the equation:
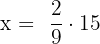
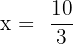
Hence, the third proportional is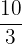 
.
Find the third proportional to 11, 13 and 26.
Suppose the third proportional is x. We can write the above numbers in proportional form like this:
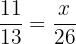
Multiply both sides by 26 to isolate x on the either side of the equation:
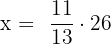
Hence, the third proportional is 22.
Find the third proportional to 3x, x + 5 and 5x - 1, if x = 2.
First, we will compute the values of these quantities like this:
First quantity = 3x = 3(2) = 6
Second quantity = x + 5 = 2 + 5 = 7
Fourth quantity = 5x - 1 = 5 (2) - 1 = 9
Suppose the third proportional is y. We can write the above numbers in proportional form like this:
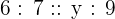
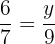
Multiply both sides by 9 to isolate y on the either side of the equation:
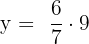
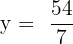
Hence, the third proportional is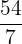 
.
Find the mean proportional between the quantities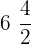 
and 9.
To find the mean proportional, we need to multiply the quantities and take the square root of them.
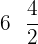is equal to 
.
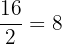The product of 8 and 9 is 72. The square root of 72 is the mean proportional of 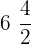and 9.
Mean Proportional = 
Find the mean proportional between the quantities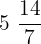 
and 225.
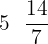is equal to 
.
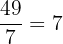First, we will take the product of 7 and 225 and then we will take the square root of the resulting term to get the mean proportional.
Mean proportional = 
= 
Find the mean proportional between the quantities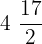 
and 50.
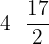is equal to 
.
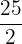First, we will take the product of 50 and 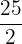and then we will take the square root of the resulting term to get the mean proportional.
Mean proportional =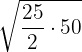 
= 
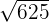
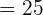
Hence, the mean proportional is 25.
Find the third proportional to 7x, x + 4 and 2x - 1, if x = 4.
First, we will compute the values of these quantities like this:
First quantity = 7x = 7(4) = 28
Second quantity = x + 4 = 4 + 4 = 8
Fourth quantity = 2x - 1 = 2 (4) - 1 = 7
Suppose the third proportional is y. We can write the above numbers in proportional form like this:
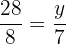
Multiply both sides by 7 to isolate y on the either side of the equation:
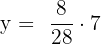
Hence, the third proportional is 2.
Find the fourth proportional to 5x + 3, 4x + 2 and 6x, if x = 1.
In this example, first, we will calculate the quantities by substituting x = 1.
First quantity = 5x + 3 = 5 (1) + 3 = 8
Second quantity = 4x + 2 = 4 (1) + 2 = 4 + 2 = 6
Third quantity = 6x = 6 (1) = 6
Suppose the fourth proportional is y. We can write the above numbers in proportional form like this:
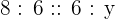
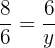
Take y on the left hand side of the equation and the fraction 
on the right hand side.
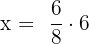
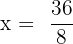
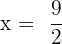
Hence, the fourth proportional is 
.
🔍 Why These Concepts Matter
These proportional relationships are not just academic exercises. They are essential tools for solving problems in:
- Similar triangles and geometric shapes (A-Level and advanced GCSE)
- Algebraic ratios and sequences
- Proportional scaling in real-life applications, such as maps, models, and physics-based problems
❌ Common Problems and Misconceptions
Understanding mean, third, and fourth proportionals can be tricky for students, especially if they're unfamiliar with setting up ratios or distinguishing between different types of averages. Below are some of the most common mistakes and misunderstandings:
1. Mixing Up the Order of Terms in Ratios
Students often reverse or misplace terms when setting up proportions. For example, when finding the fourth proportional to a, b, and c, the correct setup is:
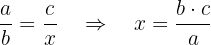
A common mistake is to write:
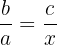
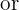
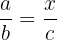
which leads to incorrect calculations.
2. Using the Arithmetic Mean Instead of the Geometric Mean
When asked to find the mean proportional, some students mistakenly calculate the arithmetic mean:
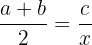
Incorrect: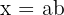 
Correction: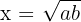 
This confusion arises because the word “mean” is often associated with averages in everyday language.
3. Forgetting to Take the Square Root
In mean proportional problems, students may correctly write:
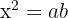
but forget to take the square root, incorrectly stating: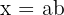
The correct solution is: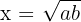
4. Incorrect Cross-Multiplication
Cross-multiplication is key to solving proportions, but errors happen. For example, starting with:
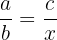
the correct steps are:
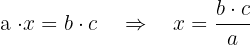
Mistakes often come from mixing terms or failing to isolate x properly.
Did you like this article? Rate it!
Loading...