Chapters
In this article, we will discuss the concept of proportions in detail. Since two ratios constitute a proportion, therefore, it is necessary to understand the concept of ratio as well as proportions.

Ratio vs Proportion
Ratio and proportion are two important concepts in mathematics that are based mostly on fractions. When we denote a fraction as a : b, then it is a ratio because it has : symbol between the two quantities. On the other hand, a proportion reflects that the two ratios are equal. For instance, consider the following equation which has two ratios:
a : b = c : d
An equality sign can be replaced by the proportion symbol :: like this:
a : b :: c : d
Here, the quantities a and d are extremos and the quantities b and c are medios.
Ratio and proportion are useful in understanding many other concepts in mathematics, science, and our daily life. For instance, we often use ratio and proportion in our daily transactions or in keeping the track of ingredients while cooking. Remember that a ratio has no unit because both the quantities are similar and their units cancel each other.
Types of Proportions
There are two types of proportions:
a) Direct Proportion
When two quantities are directly related to each other, then we say that they are directly proportional to each other. In other words, we can say that when an increase in one quantity causes an increase in the other quantity or a decrease in one quantity causes a decrease in other quantity, then the two quantities are directly proportional to each other.
If x is directly proportional to y, then we can denote it mathematically as:
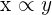
Consider the following scenario that will help you to understand the concept better:
A train covers 120 miles in one hour. In how many hours, will the train cover a distance of 360 miles?
Well, this scenario represents a direct proportionality between the variables distance and time. In lesser time, the train will cover less distance. Conversely, in more time, the train will cover the greater distance. We can write the information from this scenario like this:
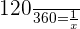
Here, x represents the number of hours required to travel 350 miles distance.
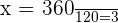 hours
hours
Hence, the train will cover 360 miles in 3 hours.
b) Inverse Proportion
When two quantities are inversely related to one another, then we say that they are inversely proportional to each other. In other words, if an increase in one quantity causes a decrease in the other quantity or a decrease in one quantity causes an increase in another quantity, then we say that the two quantities are inversely proportional to each other. Mathematically, we can denote this relationship as:

It shows that x is inversely proportional to y.
Consider the following scenario:
8 workers complete the work in 5 hours. In how many hours, will 6 workers complete the same amount of work?
Well, this scenario clearly represents a case of inverse proportionality because the two variables time and number of workers are inversely related to each other. In other words, we can say that the more the workers are, the less time it would take to complete the work and vice versa.
Now, we will solve the example by creating an equation like this:
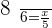
Multiply both sides by 5 to isolate x:

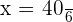
 hours
hours
Hence, 6 workers will complete the same amount of work in 6.6 hours which is approximately equal to 6 hours 36 minutes.
Now, in the next section, we will discuss what is meant by the constant of proportionality.
Third, Mean and Fourth Proportional
What is a Fourth Proportional?
Consider a proportion of two ratios a : b : : c : d. We can write this proportion as an equation a : b = c : d. The fourth quantity d is called fourth proportional to the other three quantities a, b and c. Consider the following example:
Find the fourth proportional to the values 3, 7 and 5.
Suppose that the fourth proportional is x. We can write the above quantities and x in proportional form like this:

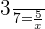
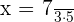
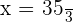
Hence, the fourth proportional is 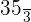 .
.
What is a Third Proportional?
Consider a proportion a : b :: c : d which can be written as an equation a:b = c:d. The third quantity c is called third proportional to the other three quantities a, b and d. Consider the following example.
Find the third proportional to 3, 7, and 9.
Suppose the third proportional is x. The above values can be written in the proportional form like this:


Multiply both the sides by 9:
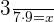

Hence, the third proportional is 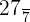 .
.
What is a Mean Proportional?
In a ratio a: b, the mean proportional is calculated by taking a square root of the product of the terms a and b. It is represented as:
Mean proportional = 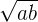
Consider the following example.
Find the mean proportional of the ratio 3 : 27
To find the mean proportional, we will multiply the values 3 and 27 together to get 81. In the end, we will take a square root of 81 to get the value of mean proportional like this:
Mean proportional = 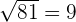
Hence, the mean proportional of the ratio 3 : 27 is 9.
Constant of Proportionality
The constant of proportionality can be defined as:
The ratio between two directly proportional quantities
For example, consider the following equation in which the quantities are directly proportional to each other:
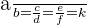
The value of the ratio, i.e. k of these ratios is known as a constant of proportionality.
In the next section, we will discuss some of the properties of proportions.
Properties of Proportions
Some of the properties of proportions are given below:
Addendo
It says that if a, b, c and d are four quantities and they are related in such a way that a : b = c : d, then a + c : b + d.
Subtrahendo
It says that if a, b, c and d are four quantities and they are related in such a way that a : b = c : d, then a - b : b = c - d : d.
Componendo
It says that if a, b, c and d are four quantities and they are related in such a way that a : b = c : d, then a + b : b = c + d : d.
Alternendo
It says that if a, b, c and d are four quantities and they are related in such a way that a : b = c : d, then a : c = b : d.
Invertendo
It says that if a, b, c and d are four quantities and they are related in such a way that a : b = c : d, then b : a : d : c.
Componendo and dividendo
It says that if a, b, c and d are four quantities and they are related in such a way that a : b = c : d, then a + b : a - b = c + d : c - d.













