Chapters
Ratio holds very importance in the mathematics world. As a matter of fact, we use ratios a lot in our daily life. For example, finding the ratio of boys and girls in a class, ingredients for cooking, detergent for the cloths, and many more. Furthermore, many complicated formulas are derived because of ratio, think what if the ratio concept was never invented?
A ratio is a quotient between two numbers or two comparable quantities which is expressed as a fraction. There are two parts in ratio, one is the antecedent (numerator) and the other is the consequent (denominator).
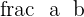
Where,
 is the antecedent,
is the antecedent,
 is the consequent.
is the consequent.
The terms of a ratio are called the antecedent and the consequent. The antecedent is the numerator and the consequent is the denominator. Basically, you are dividing "a" into equal parts but in how many parts you want? That is decided by the number "b". For example, you have a giant cake and you need to distribute that cake to five friends. In terms of ratio, the cake will "a" and the number of friends will be "b". You will write like this: 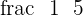 .
.

Example
The ratio of girls in a group of students is  for every 10 boys:
for every 10 boys: 
This can also be expressed using the odds notation 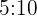 , which is read as
, which is read as  to
to  .
.
Ratios can be reduced much like fractions to a simpler form (  or
or 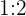 ).
).
This ratio of girls in a group expresses how many girls there are in relation to boys, however, it can also be expressed in terms of the total number of people in a group 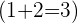 . For example,
. For example,  of every
of every  students is a girl.
students is a girl.
It is important to remember that ratios and rational numbers are not the same.
If 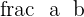 is a rational number, then a and b are integers with
is a rational number, then a and b are integers with 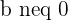 , while in the ratio
, while in the ratio 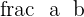 , a and b can be decimal numbers.
, a and b can be decimal numbers.













