Chapters

Exercise 1
Calculate the unknown term in the following proportions:
1 $frac {4}{10} = frac {x}{60}$
2 $frac {9}{12} = frac {12}{x}$
3 $frac {8}{32} = frac {2}{x}$
4 $frac {3}{x} = frac {x}{12}$
5 $frac {x}{6} = frac {24}{x}$
Exercise 2
Anne buys 5 pounds of potatoes at the market. If 2 pounds cost $0.80, how much will Anne pay?
Exercise 3
Calculate the height of a building that casts a shadow of 6.5 meters at the same time that a pole with a height of 4.5 m casts a shadow of 0.90 m.
Exercise 4
The legs of a right triangle measure 24 m and 10 m and its hypotenuse is 26 m. What is the length of the legs of a similar triangle whose hypotenuse is 52 m?
Exercise 5
Two wheels are connected by a transmitter belt. The first has a radius of 25 cm and the second, 75 cm. When the first has reached 300 turns, how many turns will the second have completed?
Exercise 6
Three individuals contribute $5,000, $7,500 and $9,000 which is together invested into a stock. After a year, the stock has made $6,450 on top of the capital. If the money is withdrawn, how much will each individual receive if their earnings are directly proportional to the capital originally contributed?
Solution of exercise 1
Calculate the unknown term in the following proportions:
1 $frac {4}{10} = frac {x}{60}$
$x = frac {4 cdot 60} {10} = 24$
2 $frac {9}{12} = frac {12}{x}$
$x = frac {12 cdot 12} {9} = 16$
3 $frac {8}{32} = frac {2}{x}$
$x = frac {32 cdot 2}{8} = 8$
4 $frac {3}{x} = frac {x}{12}$
$ x ^2 = 36$
$x = pm 6$
5 $frac {x}{6} = frac {24}{x}$
$x^2 = 144$
$x = pm 12$
Solution of exercise 2
Anne buys 5 pounds of potatoes at the market. If 2 pounds cost $0.80, how much will Anne pay?
The weight and the price are directly proportional because when the weight increases, the total price increases and when the weight decreases, the total price decreases.
$frac {2}{5} = frac {0.80}{x}$
$2 cdot x = 5 cdot 0.80$
$x = frac {5 times 0.80}{2} = 2$
Solution of exercise 3
Calculate the height of a building that casts a shadow of 6.5 meters at the same time, a pole with a height of 4.5 m casts a shadow of 0.90 m.

The height and the length of the shadow are directly proportional because as the height increases, so does the shadows length and as the height decreases, the length of the shadow also decreases.
$frac {0.9}{6.5} = frac {4.5}{x}$
$x = frac {6.5 times 4.5}{0.9} = 32.5 m$
Solution of exercise 4
The legs of a right triangle measure 24 m and 10 m and its hypotenuse is 26 m. What is the length of the legs of a similar triangle whose hypotenuse is 52 m?
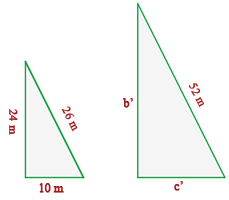
The length of legs are directly proportional to the length of the hypotenuse in the similar triangle. If the hypotenuse increases, so does the length of the legs and if the length of the hypotenuse decreases, the legs decrease as well.
$frac {26}{52} = frac {24}{b}$
$b = frac{52 times 24}{26} = 48 m$
$frac {26}{52} = frac {10}{c}$
$c = frac {52 times 10}{26} = 20 m$
Solution of exercise 5
Two wheels are connected by a transmitter belt. The first has a radius of 25 cm and the second, 75 cm. When the first has reached 300 turns, how many turns will the second have completed?
The length of the radius and the number of turns are inversely proportional because the larger the radius is, the fewer times the wheel will complete a rotation and the smaller the radius is, the more frequently the wheel will complete a rotation.
Radius Turns
25 300
75 100
$frac {75}{25} = frac {300}{x}$
$x = frac {300 times 25}{75} = 100$ turns
Solution of exercise 6
Three individuals contribute $5,000, $7,500 and $9,000 which is together invested into a stock. After a year, the stock has made $6,450 on top of the capital. If the money is withdrawn, how much will each individual receive if their earnings are directly proportional to the capital originally contributed?
The amount invested is directly proportional to the amount gained because the more money originally invested translates into a higher return and the less money originally invested translates into a lower return.
$frac {x}{5000} = frac {y}{7500} = frac {z}{9000} = frac {x + y + z}{21500} = frac {6450}{21500}$
$frac {x}{5000} = frac {6450}{21500}$
$x = frac {6450 times 5000}{21500} = $1500$
$frac {y}{7500} = frac {6450}{21500}$
$y = frac {6450 times 7500}{21500} = $2250$
$frac{z}{9000} = frac {6450}{21500}$
$z = frac {6450 times 9000}{21500} = $2700$













