Chapters
The simplest definition of interest is that it is the amount of money that is paid in addition to the amount borrowed. The total interest is directly proportional to the amount borrowed and the duration of the loan. This might be a little bit difficult to understand, let's take help from an example for more clarity. For example, Bill wants to borrow  dollars from the bank for a year and the bank told Bill that they will charge
dollars from the bank for a year and the bank told Bill that they will charge 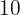 interest on the loan. It means that Bill will receive
interest on the loan. It means that Bill will receive  dollars from the bank but he needs to pay
dollars from the bank but he needs to pay 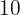 interest when returning the loan. The
interest when returning the loan. The 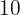 of
of  dollars is
dollars is  dollars. That
dollars. That  dollars is the "interest"(represented by "I") and
dollars is the "interest"(represented by "I") and 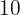 is the "interest rate"(represented by "r") but in slang, people still consider
is the "interest rate"(represented by "r") but in slang, people still consider 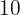 as interest. It means that when Bill will return
as interest. It means that when Bill will return  dollars to the bank, after a year, he also needs to pay the interest hence he needs to pay
dollars to the bank, after a year, he also needs to pay the interest hence he needs to pay  dollars to the bank. In that
dollars to the bank. In that  dollars, Bill paid interest + the amount borrowed.
dollars, Bill paid interest + the amount borrowed.
The amount borrowed is called the principal(represented by "P"). In conclusion, Bill paid interest + principal after a year to the bank. Since we talked about special words, there are special words for Bill and the bank as well. We will call Bill as the Borrower and the bank will be Lender. There is another problem, in this whole example, we consider the time period as one year, what if Bill wants to borrow for two years? The question is, will this affect interest? Yes, it will. The bank offered 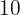 interest rate for a year, which means that if the number of years changes, so will the interest. At that time, Bill would pay
interest rate for a year, which means that if the number of years changes, so will the interest. At that time, Bill would pay  dollars after a year but now(since he is borrowing for two years), he needs to pay
dollars after a year but now(since he is borrowing for two years), he needs to pay  dollars for two years. To calculate interest in an easy way, we have a formula that will calculate interest which is:
dollars for two years. To calculate interest in an easy way, we have a formula that will calculate interest which is:
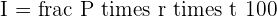 (If time is expressed in years)
(If time is expressed in years)
Where:
| Concept | Name | Symbol |
|---|---|---|
| Amount borrowed | Principal | P |
| Loan duration | Time | t |
| Interest rate | Rate | r |
| Additional amount | Interest | I |
However, the above formula is specified for the interest calculated for years. Every bank has a different interest calculating system, some calculate it in years, while some in months, and you might be a bit surprised to know that some calculate it in days. Does that affect the above formula? Yes, it does but don't worry, if you want to calculate the interest in months then use the below formula:
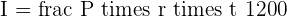 (If time is expressed in months)
(If time is expressed in months)
And if you want to calculate the interest in days then:
 (If time is expressed in days)
(If time is expressed in days)

Examples
Calculate the amount of simple interest that is paid over a period of five years on a principal of 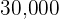 dollars at a simple interest rate of
dollars at a simple interest rate of 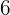 .
.
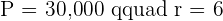
Since the time is in years:
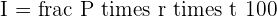
 dollars
dollars
Calculate the total amount paid in six months on a principal of 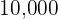 dollars at a simple interest rate of
dollars at a simple interest rate of  .
.
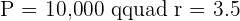
Since the time is in months:
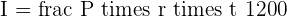
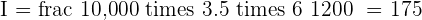 dollars
dollars
Total amount = 
How long will it take a principal of 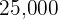 dollars at a simple interest rate of
dollars at a simple interest rate of  to become
to become 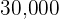 dollars?
dollars?

Since the time is in years:
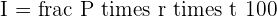
And we need to find time then:
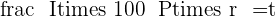
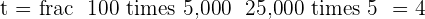 years
years












