Chapters
What are Binomial Coefficients?
The positive integers that are coefficients in the binomial theorem are known as binomial coefficients. A combination is also known as a combinatorial number or a binomial coefficient. Combinations and permutations are used to compute the total number of possible outcomes from a given set. The only difference between the combination and permutation is that the order does not matter in combinations and matters in permutations. In this article, we will learn and solve examples related to binomial coefficients.
The general notation along with the formula of the binomial coefficient is given below:
, where 
We can read it as "n over k", or sometimes "n choose k". It is denoted as 
.
It reflects the number of ways we can choose unordered k outcomes from "n" number of possibilities. Therefore, they are also known as the combination or combinatorial numbers. In the next section, we will see what are the properties of binomial coefficients.
Properties of Binomial Coefficients
These coefficients are derived from Blaise Pascal's well-known triangle known as Pascal's triangle. They help in doing a combinatorial analysis. In this section, we will discuss some of the properties of binomial coefficients.
Symmetry Property
For example:
Special Cases
For instance,
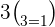
Pascal's Rule
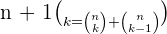
For instance,
Negated Upper Index of Binomial Coefficient
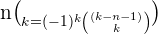
For instance:
Now, we know what are binomial coefficients and their properties, we will proceed to solve some of the examples related to binomial coefficients.
Example 1
Solve 
Solution
Use the following rule to solve this example:
, where
Substitute the values of n and k in the above formula like this:
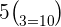
Example 2
Solve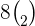 
Solution
Use the following rule to solve this example:
, where
Substitute the values of n and k in the above formula like this:
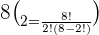
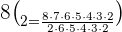
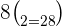
Example 3
Solve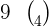 
Solution
We know that 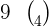can be written as:
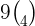
We will use the following formula to solve this example:
, where
To calculate the answer, substitute the values of n and k in the above formula:
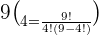
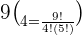
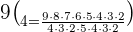
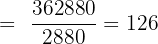
Example 4
Suppose you have got 3 free tickets for a theme park and you have 7 friends and family members who want to come with you.
In how many ways can you make the groups of friends and family members to take with you to the theme park?
Solution
First, try to understand the problem. 7 people want to go with you to the theme park. But, you have just got 3 free tickets. It means you can only take 3 people with you. Now, in this question, we are asked to tell the number of groups that can be formed from this available data.
We can write this question like this in combinatorics form:
We will use the following formula to get the number of groups that can be formed from a group of 7 people:
, where
Substitute the values in the above formula to get all possible combinations of people who can accompany you to the park:
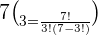
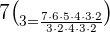
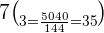
Hence, you can form 35 different groups from the list of 7 people given the constraint that only 3 people can accompany you to the park.
Example 5
Suppose you have to paint a wall. From 10 colors, you can pick only 5 colors. How many combinations of colors are possible?
Solution
First, we will try to comprehend the problem. We have 10 colors and you have to choose a number of ways you can paint the wall by picking up 5 colors only. In other words, we can say that we can make different combinations by choosing 5 colors from 10 colors.
We can write this question like this in combinatorics form:
We will use the following formula to get the number of groups that can be formed from a group of 7 people:
, where
Substitute the values in the above formula to get the number of arrangements:
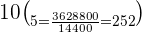
Hence, you can paint the wall in 252 different ways by picking up 5 colors at a single time from a group of 10 colors.
Example 6
Sam has to choose a combination of three flavors of ice cream from 10 flavors. How many different combinations of ice cream can he choose from 10 flavors?
Solution
Let us understand this problem first by breaking down its elements.
There are 10 ice cream flavors and Sam has to choose 3 flavors. The problem asks us to tell the number of different combinations that can be made from 10 flavors of ice-cream given the fact that a person can have only 3 flavors.
We can write this question like this in combinatorics form:
We will use the following formula to get the number of ice-cream combinations that can be formed from 10 flavors:
, where
Substitute the values in the above formula:
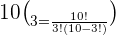
Hence, Sam can make 120 different combinations of ice-cream flavors from 10 flavors, given that he can only choose 3 at a time.
Example 7
John has to make a group of 4 students in the class to represent the school in a science fair. There are total 15 students in the class. If a group should have four students, how many different combinations of groups John can make from a class of 15 students by picking 4 students at random?
Solution
Let us understand this problem first by breaking down its elements.
There are 15 students in the class. The group should be constituted of 4 students and John needs to select these four students from a class of 15 students.
We can write this question like this in combinatorics form:
We will use the following formula to get the number of ice-cream combinations that can be formed from 10 flavors:
, where
Substitute the values in the above formula:
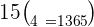
The binomial coefficient equals to 1365, that shows that John can make the group in 1365 ways from a class of 15 students, given that the group has only four members.
Did you like this article? Rate it!
Loading...
There are many source to learn the statistics subject but this platform is most important and good as compare to others.thanks
In TSC Exam, There are 50 questions. Each question has four alternative answers following it and the student must select the correct answer. Two marks are given for correct answer and 0.4 marks reduced for every wrong answer. A student must score at least 50% of maximum possible marks to pass the exam. Suppose that a student has not studied at all that he decides to select the answer to question on random basis. What is the probability that he will in the examination?
In question 3 : i think you have missed 9 . it should be (10*9)/2 (1/5)^2(4/5)^8
good job
Can you give me 5 real-life problems involving random variables?
i need it now please
A) 0.2668
B) 0.33965
C) 0,04575
D) 0.97175
Hello please
Can you please help me with question 6?
Thank you
A) 0.2668
B) 0.33965
C) 0,04575
D) 0.97175