Chapters
Sometimes, probability can mess up your head. You will see a number of values with different probabilities, therefore, interpreting with them becomes difficult. That is why the concept of distribution function was born. This mathematical expression shows the chances of occurring of a specific value or a set of values. Suppose that the X is a discrete random variable with values in  . These values are sorted from lowest to highest, the distribution function of the variable X is:
. These values are sorted from lowest to highest, the distribution function of the variable X is:

The distribution function associates the cumulative probability of each value of the random variable. In addition, the distribution function is also commonly referred to as the cumulative distribution function. You must be wondering why the distribution function is important? Many statisticians use the distribution function because it makes sense for any sort of random variable. It doesn't matter whether the distribution is mixed, continuous, or discrete, it will help them to understand that function properly. Furthermore, the distribution function determines the distribution of the X.

Properties
Below are the properties of cumulative distribution function:

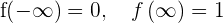
- In case, if
 that means
that means 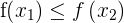
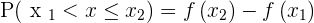
Since we know that we are dealing with probability here, this means that the values of  will range from 0 to 1. In addition, the value of x can be any real number from
will range from 0 to 1. In addition, the value of x can be any real number from  to
to  . In the second property, if we input
. In the second property, if we input  as the value of x in the original equation that will be
as the value of x in the original equation that will be 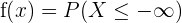 . This is not possible since distribution of the X should always be lesser than x (any real number) and there is nothing smaller than
. This is not possible since distribution of the X should always be lesser than x (any real number) and there is nothing smaller than  , therefore, we will say the probability of that occurring is
, therefore, we will say the probability of that occurring is  . On the other hand,
. On the other hand,  , this means distribution of the X is less than infinity, without any doubt, there is nothing greater than infinity and that is why probability of that occurring is
, this means distribution of the X is less than infinity, without any doubt, there is nothing greater than infinity and that is why probability of that occurring is  .
.
Suppose 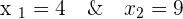 , in this case, the cumulative distribution at
, in this case, the cumulative distribution at 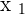 will be less than or it could be equal to cumulative distribution at
will be less than or it could be equal to cumulative distribution at  . In simple words, as the number increases from left to right, the
. In simple words, as the number increases from left to right, the  function will keep getting bigger or it will stay the same but one thing is for sure, it will never get smaller than
function will keep getting bigger or it will stay the same but one thing is for sure, it will never get smaller than 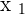 . The last property says, what is the probability of the random variable between two different numbers? To find that you will need to subtract the distributive function of
. The last property says, what is the probability of the random variable between two different numbers? To find that you will need to subtract the distributive function of 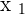 from the distributive function of
from the distributive function of  (don't forget that these functions are probabilities and the answer will never exceed from one).
(don't forget that these functions are probabilities and the answer will never exceed from one).
Example
Q.1 Calculate the probability distribution function for the probable scores that can be obtained by throwing a die.
 | 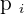 |
|---|---|
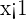 |  |
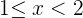 |  |
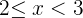 | 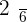 |
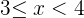 | 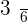 |
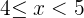 | 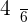 |
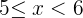 | 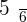 |
 |  |
Representation
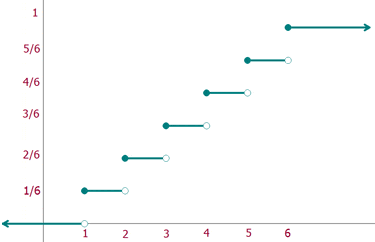
Q.2 Given the probability distribution for random variable X, find the cumulative distribution and find 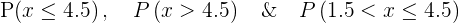
 |  |  |  |  |
|---|---|---|---|---|
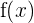 |  |  |  |  |

Remember, the small x donates a random number. It means that whatever will be the value of x will be the value of 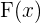

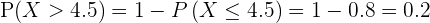
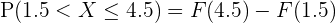















There are many source to learn the statistics subject but this platform is most important and good as compare to others.thanks
In TSC Exam, There are 50 questions. Each question has four alternative answers following it and the student must select the correct answer. Two marks are given for correct answer and 0.4 marks reduced for every wrong answer. A student must score at least 50% of maximum possible marks to pass the exam. Suppose that a student has not studied at all that he decides to select the answer to question on random basis. What is the probability that he will in the examination?
In question 3 : i think you have missed 9 . it should be (10*9)/2 (1/5)^2(4/5)^8
good job
Can you give me 5 real-life problems involving random variables?
i need it now please
A) 0.2668
B) 0.33965
C) 0,04575
D) 0.97175
Hello please
Can you please help me with question 6?
Thank you
A) 0.2668
B) 0.33965
C) 0,04575
D) 0.97175