Chapters
Expected value is one of the most used statistical methods to predict the future of anything. The expected value of a discrete random variable is the sum of the product of the probability of each event by the value of that event. Let's simplify the above statement. As the word "Expected" tells you that we expect the return for any kind of action, whether it is related to business or anything else such as how many questions you might get wrong or right in an exam, etc. (We will use this example again to show how expected value works in an MCQ exam).

Expected Value Formula
To calculate the expected value, you will require two things. The first one is the probability (chance of a certain action occurring) and the number of samples. The probability is denoted by p and the number of samples is denoted by n. Below is the formula to calculate the expected value.
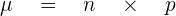
Basically, the expected value formula is the product of the probability of any event and the number of times the event happens. Although the formula varies according to the number of events. In most cases, either you will be using the expected value formula of a binomial random variable or you might use the expected value formula for the multiple events. Sometimes, the expected value is denoted by 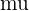 but in some textbooks, you might find
but in some textbooks, you might find  instead of
instead of  .
.
Expected Value Formula of a Binomial Random Variable
Below is the formula for the expected value of a binomial random variable:
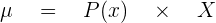
Where  is the probability of success and
is the probability of success and  is the number of trails. Let's inherit the MCQ example here, an exam has 20 multiple questions and there are 4 options (which are A, B, C, and D). The student can only choose one answer and out of the 4 options, only one option is correct. It means that the probability of success will be
is the number of trails. Let's inherit the MCQ example here, an exam has 20 multiple questions and there are 4 options (which are A, B, C, and D). The student can only choose one answer and out of the 4 options, only one option is correct. It means that the probability of success will be  and the number of trails is
and the number of trails is  . The expected value will be:
. The expected value will be:
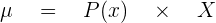

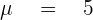
Here is another example, a coin is tossed 5 times. The probability of getting a tail is 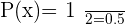 . The expected value (the number of tails that you can expect) is:
. The expected value (the number of tails that you can expect) is:
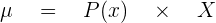
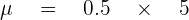

Expected Value Formula of Multiple Events
Calculating the expected value in real life is more complicated than you think. For example, you bought a ticket for an art valued at 10,000 dollars. One thousand tickets are sold, what is the expected value of your gain? So, the formula changes to calculate the expected value where there are many possibilities is:

When we are talking about multiple events, we talk about many probabilities. In the above example, there will be people who bought multiple tickets, there might be people who bought only one ticket, and these possibilities go on. To find the expected value for you, you need to find individual products of their probability and number of their tickets (that people bought) and then you need to sum all of the products and that is why we use summation notation.
Variance of a Discrete Random Variable
Calculating variance is pretty simple in the case of the discrete random variable. To calculate variance, first, you need to square all "number of events occurring" (which is denoted by 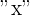 ). Then you need to multiply all the squared x values with their individual probabilities (
). Then you need to multiply all the squared x values with their individual probabilities (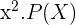 ). Then the next step is to sum all the
). Then the next step is to sum all the 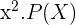 (in other words,
(in other words, 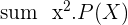 ). Last but not least, subtract the answer that you obtained by the
). Last but not least, subtract the answer that you obtained by the 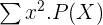 from the squared value of mu (i.e.
from the squared value of mu (i.e. 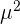 ).
).

Standard Deviation of a Discrete Random Variable
To calculate the standard deviation of a discrete random variable, you have to find the variance. Once you find the variance, simply take a square root of the value and that is how you find the standard deviation.
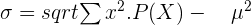
Example
Calculate the expected value, variance, and standard deviation of the probability distribution for the possible outcomes that can be obtained by throwing a die.
 | 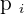 | 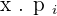 | 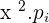 |
|---|---|---|---|
 |  |  |  |
 |  | 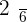 | 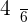 |
 |  | 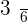 | 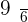 |
 |  | 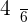 | 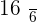 |
 |  | 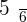 | 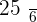 |
 |  | 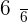 | 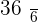 |
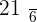 | 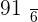 |

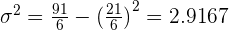
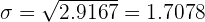













There are many source to learn the statistics subject but this platform is most important and good as compare to others.thanks
In TSC Exam, There are 50 questions. Each question has four alternative answers following it and the student must select the correct answer. Two marks are given for correct answer and 0.4 marks reduced for every wrong answer. A student must score at least 50% of maximum possible marks to pass the exam. Suppose that a student has not studied at all that he decides to select the answer to question on random basis. What is the probability that he will in the examination?
In question 3 : i think you have missed 9 . it should be (10*9)/2 (1/5)^2(4/5)^8
good job
Can you give me 5 real-life problems involving random variables?
i need it now please
A) 0.2668
B) 0.33965
C) 0,04575
D) 0.97175
Hello please
Can you please help me with question 6?
Thank you
A) 0.2668
B) 0.33965
C) 0,04575
D) 0.97175