Chapters

Exercise 1
A coin is tossed four times. Calculate the probability of obtaining more heads than tails.
Exercise 2
An agent sells life insurance policies to five equally aged, healthy people. According to recent data, the probability of a person living in these conditions for 30 years or more is 2/3. Calculate the probability that after 30 years:
1. All five people are still living.
2. At least three people are still living.
3. Exactly two people are still living.
Exercise 3
If from six to seven in the evening one telephone line in every five is engaged in a conversation: what is the probability that when 10 telephone numbers are chosen at random, only two are in use?
Exercise 4
The probability of a man hitting the target at a shooting range is 1/4. If he shoots 10 times, what is the probability that he hits the target exactly three times? What is the probability that he hits the target at least once?
Exercise 5
There are 10 red and 20 blue balls in a box. A ball is chosen at random and it is noted whether it is red. The process repeats, returning the ball 10 times. Calculate the expected value and the standard deviation of this game.
Exercise 6
It has been determined that 5% of drivers checked at a road stop show traces of alcohol and 10% of drivers checked do not wear seat belts. In addition, it has been observed that the two infractions are independent from one another. If an officer stops five drivers at random:
1. Calculate the probability that exactly three of the drivers have committed any one of the two offenses.
2. Calculate the probability that at least one of the drivers checked has committed at least one of the two offenses.
Exercise 7
A pharmaceutical lab states that a drug causes negative side effects in 3 of every 100 patients. To confirm this affirmation, another laboratory chooses 5 people at random who have consumed the drug. What is the probability of the following events?
1. None of the five patients experience side effects.
2.At least two experience side effects.
3.What is the average number of patients that the laboratory should expect to experience side effects if they choose 100 patients at random?
Solution of exercise 1
A coin is tossed four times. Calculate the probability of obtaining more heads than tails.


Solution of exercise 2
An agent sells life insurance policies to five equally aged, healthy people. According to recent data, the probability of a person living in these conditions for 30 years or more is 2/3. Calculate the probability that after 30 years:
1. All five people are still living.

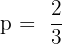
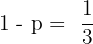
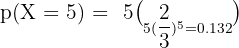
2. At least three people are still living.

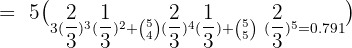
3. Exactly two people are still living.

Solution of exercise 3
If from six to seven in the evening one telephone line in every five is engaged in a conversation: what is the probability that when 10 telephone numbers are chosen at random, only two are in use?
B(10, 1/5)p = 1/51 − p = 4/5

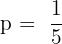
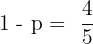
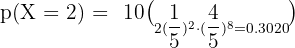
Solution of exercise 4
The probability of a man hitting the target at a shooting range is 1/4. If he shoots 10 times, what is the probability that he hits the target exactly three times? What is the probability that he hits the target at least once?
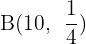
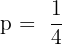
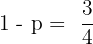
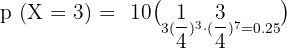
p (at least one) =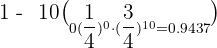
Solution of exercise 5
There are 10 red and 20 blue balls in a box. A ball is chosen at random and it is noted whether it is red. The process repeats, returning the ball 10 times. Calculate the expected value and the standard deviation of this game.
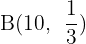

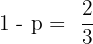


Solution of exercise 6
It has been determined that 5% of drivers checked at a road stop show traces of alcohol and 10% of drivers checked do not wear seat belts. In addition, it has been observed that the two infractions are independent from one another. If an officer stops five drivers at random:
1. Calculate the probability that exactly three of the drivers have committed any one of the two offenses.





2. Calculate the probability that at least one of the drivers checked has committed at least one of the two offenses.
p (at least one) = 
Solution of exercise 7
A pharmaceutical lab states that a drug causes negative side effects in 3 of every 100 patients. To confirm this affirmation, another laboratory chooses 5 people at random who have consumed the drug. What is the probability of the following events?
1. None of the five patients experience side effects.




2. At least two experience side effects.


3. What is the average number of patients that the laboratory should expect to experience side effects if they choose 100 patients at random?














There are many source to learn the statistics subject but this platform is most important and good as compare to others.thanks
In TSC Exam, There are 50 questions. Each question has four alternative answers following it and the student must select the correct answer. Two marks are given for correct answer and 0.4 marks reduced for every wrong answer. A student must score at least 50% of maximum possible marks to pass the exam. Suppose that a student has not studied at all that he decides to select the answer to question on random basis. What is the probability that he will in the examination?
In question 3 : i think you have missed 9 . it should be (10*9)/2 (1/5)^2(4/5)^8
good job
Can you give me 5 real-life problems involving random variables?
i need it now please
A) 0.2668
B) 0.33965
C) 0,04575
D) 0.97175
Hello please
Can you please help me with question 6?
Thank you
A) 0.2668
B) 0.33965
C) 0,04575
D) 0.97175