Chapters
A discrete probability distribution is composed of discrete variables and it elaborates the likelihood of the occurrence of each value of a discrete random variable. If you have studied statistics before, then you may be familiar with many different types of probability distributions, for instance, binomial distribution, normal distribution, and Poisson distribution. We categorize all of these distributions either as a continuous or discrete probability distribution.
A random variable whose values can be enumerated is known as a discrete random variable. For example, a set of non-negative integers can be counted, therefore the entire set is a discrete random variable.
We match each random variable value with a non-zero probability in a discrete probability distribution. Discrete probability distributions are often given in the form of a table. The probability distribution is also known as the probability function or the probability mass function.
Expected Value Function
We can use the expected value function in discrete probability problems to calculate the mean or expected value. In other words, we can say that the expected value of the function means calculating its average. The expected value function is mathematically denoted as E(x) and has the following formula:
It means that each value of 
is multiplied by its corresponding probability and all the values are added in the end to get the expected value.
Discrete Probability Distribution Examples
- Friends rolling a dice. If anyone rolls a six, he/she will win.
- The number of chocolates in a packet.
- The number of traffic accidents in a city on any given day.
- The number of students absent from school in five days of the week.
- The number of customers visiting a restaurant in a month.
- The number of students graduating from a college in each year.
- If there is heads up after flipping a coin, then a student will get a chocolate.
Rolling a die - Example
For example, if a die is rolled, then the probability of each outcome is represented by the following table:
| Number | Probability |
|---|---|
| 1 | 1/6 |
| 2 | 1/6 |
| 3 | 1/6 |
| 4 | 1/6 |
| 5 | 1/6 |
| 6 | 1/6 |
You can see that in the above table, each value has the same possible outcome. Now, let us calculate the expected value function of the above probability distribution. The formula for the expected value of a function is given below:
We will multiply 
with each corresponding value of X and add all the values together to get the expected value function.
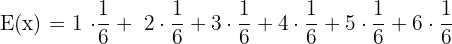
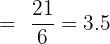
The expected value helps us to determine the average value after the number of trials in an experiment. Of course, the value of the die cannot be 3.5, but we often get a decimal value while computing the expected value function.
Representation of the Probability Distribution
The below bar chart represents the possible outcomes of rolling a die.
You can see that the probability of all the outcomes is the same. Now, let us see how to compute the expected value function and values of functions.
Example 1
The number of customers visiting a shop on the first five days of the week is given in the tabular form below.
| Day | Number of Customers | Probability |
|---|---|---|
| 1 | 20 | 0.20 |
| 2 | 10 | 0.10 |
| 3 | 30 | 0.30 |
| 4 | 10 | 0.10 |
| 5 | 30 | 0.30 |
Calculate the expected value function.
Solution
The formula for computing the expected value function is given below:
We will multiply the number of customers visiting the shop each day with its corresponding probability. In the end, we will enumerate all the values to get the expected number of customers who can visit the shop on a particular day.
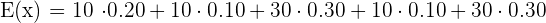
Hence, an average of 24 customers can visit a shop on a particular day.
Example 2
The discrete probability distribution of the variable Z is given in the form of the following table:
| Z | Probability |
|---|---|
| 26 | 0.35 |
| 28 | 0.10 |
| 32 | 0.15 |
| 35 | 0.30 |
| 38 | 0.10 |
Compute the following values:
1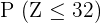 
2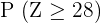 
3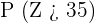 
Solution
1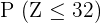
To compute this value, we will count the probabilities of all the values of Z that are less than and equal to 32. Since we have 
sign, therefore we will also count the probability of 32 in the final answer.
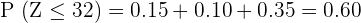
2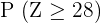
To compute this value, we will count the probabilities of all the values of Z that are greater than or equal to 28. Since we have 
sign, therefore we will also count the probability of 28 in the final answer.
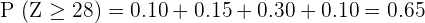
3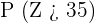
To compute this value, we will count the probabilities of all the values of Z that are greater than 35. Since we only have a greater than symbol, hence we will not count the probability of 35.
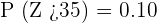
Example 3
Compute the expected value function or mean from the following table which shows the number of accidents occurring in a city in five days of the week.
| Day | Number of accidents |
|---|---|
| 1 | 50 |
| 2 | 75 |
| 3 | 25 |
| 4 | 60 |
| 5 | 40 |
Solution
To calculate the mean value of accidents happening in a city, we need to compute the probability of each day like this:
Total number of accidents = 50 + 75 + 25 + 60 + 40 = 250
Probability of Day 1 =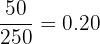 
Probability of Day 2 =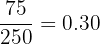 
Probability of Day 3 =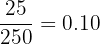 
Probability of Day 4 =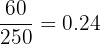 
Probability of Day 5 =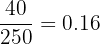 
After adding all of the above probabilities, the final answer should be 1.
The formula for computing the expected value function is given below:
We will multiply each probability with its corresponding value. Finally, we will add all the values together to get the expected value function.
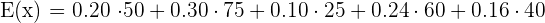
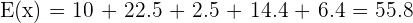
Example 4
The discrete probability distribution of the variable X is given in the form of the following table:
| X | Probability |
|---|---|
| 11 | 0.21 |
| 13 | 0.19 |
| 15 | 0.46 |
| 18 | 0.14 |
Compute the following values:
1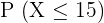 
2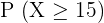 
3 
Solution
1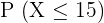
To compute this value, we will count the probabilities of all the values of X that are less than and equal to 15. Since we have sign, therefore we will also count the probability of 15 in the final answer.
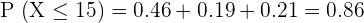
2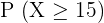
To compute this value, we will count the probabilities of all the values of X that are greater than and equal to 15. Since we have sign, therefore we will also count the probability of 15 in the final answer.
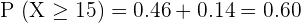
3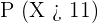 
To compute this value, we will count the probabilities of all the values of X that are greater than 11. Since we only have a greater than symbol, hence we will not count the probability of 11.
Did you like this article? Rate it!
Loading...
There are many source to learn the statistics subject but this platform is most important and good as compare to others.thanks
In TSC Exam, There are 50 questions. Each question has four alternative answers following it and the student must select the correct answer. Two marks are given for correct answer and 0.4 marks reduced for every wrong answer. A student must score at least 50% of maximum possible marks to pass the exam. Suppose that a student has not studied at all that he decides to select the answer to question on random basis. What is the probability that he will in the examination?
In question 3 : i think you have missed 9 . it should be (10*9)/2 (1/5)^2(4/5)^8
good job
Can you give me 5 real-life problems involving random variables?
i need it now please
A) 0.2668
B) 0.33965
C) 0,04575
D) 0.97175
Hello please
Can you please help me with question 6?
Thank you
A) 0.2668
B) 0.33965
C) 0,04575
D) 0.97175