Chapters

Exercise 1
Exercise 2
Exercise 3
Exercise 4
Exercise 5
Exercise 6
Solution of exercise 1
Solution of exercise 2
Solution of exercise 3
Solution of exercise 4
Solution of exercise 5
Solution of exercise 6

The best Maths tutors available

Exercise 1

A pair of a die is thrown. The random variable, X, is defined as the sum of the obtained scores. Determine the probability distribution, the expected value, and variance.

Exercise 2

A player throws a die. If a prime number is obtained, he gains to win an amount equal to the number rolled times 100 dollars, but if a prime number is not obtained, he loses an amount equal to the number rolled times 100 dollars. Calculate the probability distribution and the expected value of the described game.

Exercise 3

The first prize for a raffle is 5,000 dollars (with a probability of 0.001) and the second prize is 2,000 dollars (with a probability of 0.003). What is a fair price to pay for a single ticket in this raffle?

Exercise 4

Let X be a discrete random variable whose probability distribution is as follows:

$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$

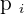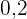1. Calculate the distribution function.

2. Calculate the following probabilities:

$\text{[math]}$

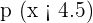
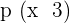
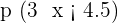
Exercise 5

A player tosses two coins into the air. He wins 1 dollar for the number of heads he will get. However, he will lose 5 dollars if neither coin is a head. Calculate the expected value of this game and determine whether it is favorable for the player.

Exercise 6

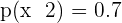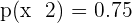Knowing that $\text{[math]}$ and $\text{[math]}$ . Calculate:

1. The expected value.

2.The variance.

3.The standard deviation.

Solution of exercise 1

A pair of die is thrown. The random variable, X, is defined as the sum of the obtained scores. Determine the probability distribution, the expected value and variance.

$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
		$\text{[math]}$	$\text{[math]}$

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

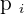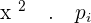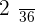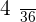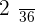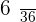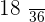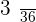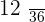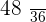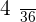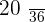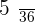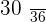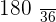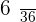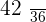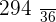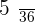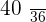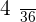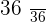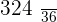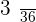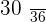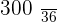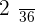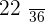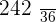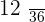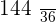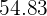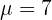
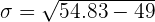
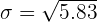
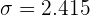
Solution of exercise 2

$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
		$\text{[math]}$

$\text{[math]}$

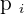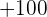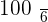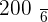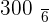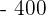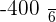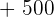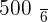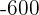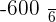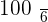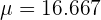
Solution of exercise 3

$\text{[math]}$

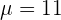$\text{[math]}$ dollars

Solution of exercise 4

Let X be a discrete random variable whose probability distribution is as follows:

$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$

$\text{[math]}$

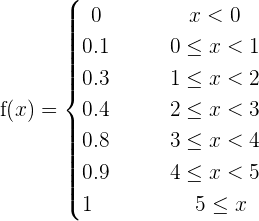
1. Calculate the distribution function.

2. Calculate the following probabilities:

$\text{[math]}$

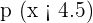
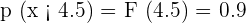
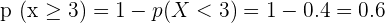
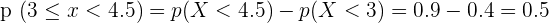
Solution of exercise 5

$\text{[math]}$

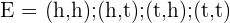
Probablity of getting 1 head= 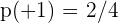$\text{[math]}$

Probablity of getting 2 heads= $\text{[math]}$

Probablity of getting two tails= $\text{[math]}$

$\text{[math]}$ $\text{[math]}$

$\text{[math]}$

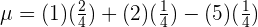
Hence, it is unfavorable.

Solution of exercise 6

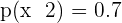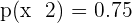Knowing that $\text{[math]}$ and $\text{[math]}$ . Calculate:

1. The expected value.

2.The variance.

3.The standard deviation.

$\text{[math]}$

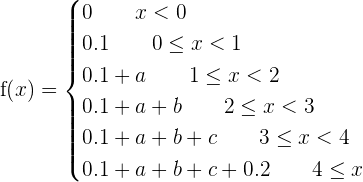
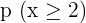
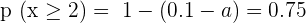
After solving the above equations simultaneously, the value of a will be "0 " and the value of b will be "0.45".

$\text{[math]}$

$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
		$\text{[math]}$	$\text{[math]}$

$\text{[math]}$

Did you like this article? Rate it!

4.00 (10 rating(s))

Emma

I am passionate about travelling and currently live and work in Paris. I like to spend my time reading, gardening, running, learning languages and exploring new places.

Leave us a comment

Cancel reply

Muhammad jahanzeb

October 2024

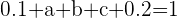
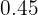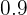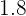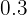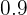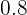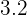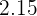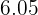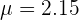
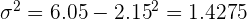
There are many source to learn the statistics subject but this platform is most important and good as compare to others.thanks

damodar

June 2024

In TSC Exam, There are 50 questions. Each question has four alternative answers following it and the student must select the correct answer. Two marks are given for correct answer and 0.4 marks reduced for every wrong answer. A student must score at least 50% of maximum possible marks to pass the exam. Suppose that a student has not studied at all that he decides to select the answer to question on random basis. What is the probability that he will in the examination?

vikhyat

January 2023

In question 3 : i think you have missed 9 . it should be (10*9)/2 (1/5)^2(4/5)^8

rajjaa

April 2022

good job

Christopher

February 2022

Can you give me 5 real-life problems involving random variables?
i need it now please

malek

November 2021

A) 0.2668
B) 0.33965
C) 0,04575
D) 0.97175

Alice Kazoozu

October 2021

Hello please
Can you please help me with question 6?
Thank you

malek

November 2021

A) 0.2668
B) 0.33965
C) 0,04575
D) 0.97175

Expected Value Word Problems

Exercise 1

Exercise 2

Exercise 3

Exercise 4

Exercise 5

Exercise 6

Solution of exercise 1

Solution of exercise 2

Solution of exercise 3

Solution of exercise 4

Solution of exercise 5

Solution of exercise 6

Random Variable

Binomial Distribution

Distribution Function

Expected Value

Binomial Coefficient

Discrete Probability Distributions