Chapters
- 1. Solve a Triangle Knowing: One Side and Two Adjacent Angles.
- Example
- 2. Solve a Triangle Knowing Two Sides and an Included Angle.
- Example
- 3. Solve a Triangle Knowing Two Sides and the Opposite Angle.
- 1. sin B > 1. No solution
- 2. sin B = 1. One Solution: Right Triangle
- 3. sin B < 1. One or Two Solutions
- 4. Solve a Triangle Knowing Two Sides and the Opposite Angle.
Triangle is a shape in the world of geometry. The word triangle can be broken into two parts. The first part is the tri and it means three and the second part is the angle. Hence, the meaning of triangle is a geometry of three lines which are making three angles. However, there are a few types of a triangle that differentiate from other triangles. The variation you will find will be in angles and lengths. Below are the types of triangles:
- Equilateral Triangle
- Isosceles Triangle
- Oblique Triangle
An oblique triangle does not have a right angle and can also be classified as an acute triangle or an obtuse triangle. The specialty of an oblique triangle is that it has all different angles and different lengths.
To solve oblique triangles, use the laws of sine and cosine. There are four different potential scenarios:

1. Solve a Triangle Knowing: One Side and Two Adjacent Angles.
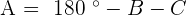



Example
Solve the oblique triangle with the following data: 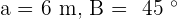 and
and 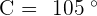 .
.

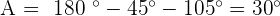
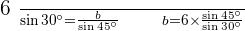
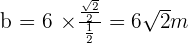
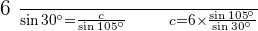
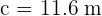
2. Solve a Triangle Knowing Two Sides and an Included Angle.


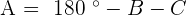

Example
Solve the oblique triangle with the following data: 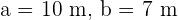 and
and  °.
°.
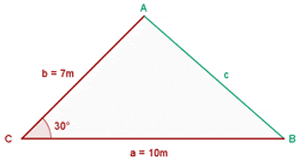
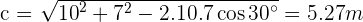

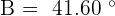 because
because 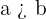 and that is why, obtuse angle is A.
and that is why, obtuse angle is A.
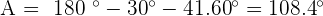
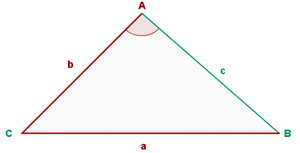
3. Solve a Triangle Knowing Two Sides and the Opposite Angle.
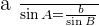 , If:
, If:
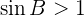 will result in no solution.
will result in no solution.
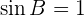 will result in one solution.
will result in one solution.
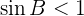 will result in one or two solutions.
will result in one or two solutions.
1. sin B > 1. No solution
Solve the triangle with the following data: 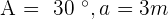 and
and  .
.
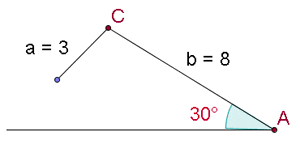
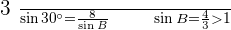
Since the sine of an angle can never be greater than 1, the problem has no solution. The drawing above shows the impossibility of the situation.
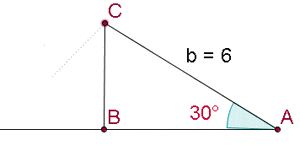
2. sin B = 1. One Solution: Right Triangle
Solve the triangle with the following data: 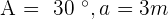 , and
, and  .
.
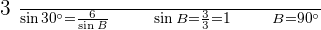
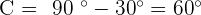
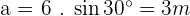

3. sin B < 1. One or Two Solutions
Solve the triangle with the following data:  , and
, and 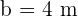 .
.
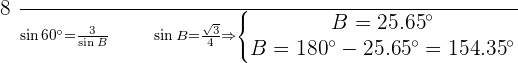
As  there is one solution which is
there is one solution which is 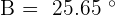


Solve the triangle with the following data: 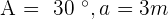 , and
, and 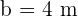 .
.
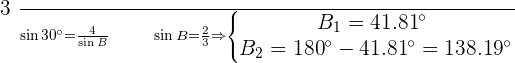
As  therefore, there are two solutions:
therefore, there are two solutions:
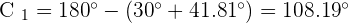
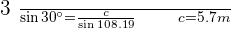
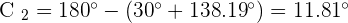

4. Solve a Triangle Knowing Two Sides and the Opposite Angle.
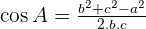
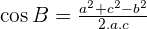
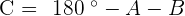
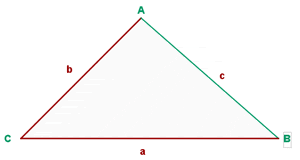
Solve the triangle with the following data: 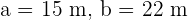 , and
, and 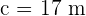 .
.
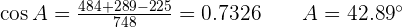

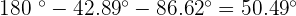
Summarise with AI:













It was good and worth learning