Chapters
Trigonometric ratios behave in different quadrants. In some cases, they behave the same as well and that is why it becomes necessary for us to understand their behavior. To understand the quadrant effect on trigonometric ratios, you need to understand a few trigonometric identities. These trigonometric identities are split into different types:
- Acute Angles Trigonometric Identities
- Supplementary Angles Trigonometric Identities
- Angles Greater Than
 or
or 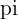 Trigonometric Identities
Trigonometric Identities - Angles Greater Than
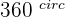 or
or  Trigonometric Identities
Trigonometric Identities - Angles That Differ by
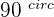 or
or  Trigonometric Identities
Trigonometric Identities - Angles That Add Up to
 or
or  Trigonometric Identities
Trigonometric Identities - Angles That Differ by
 or
or  Trigonometric Identities
Trigonometric Identities

The best Maths tutors available
Supplementary Angles
Two angles are supplementary if the sum is  or
or 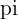 radians. So, if two supplementary Angles are added, a straight angle is obtained.
radians. So, if two supplementary Angles are added, a straight angle is obtained.
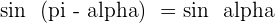

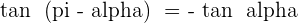

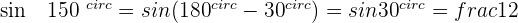

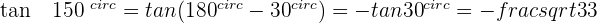
Angles That Differ by 180° or π Rad
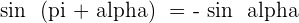

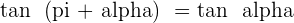
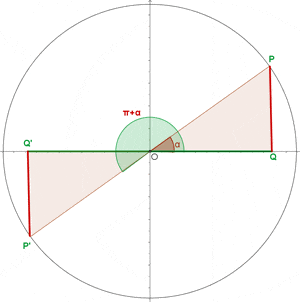
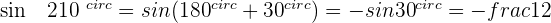

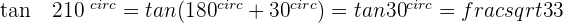
Angles Greater Than 360º
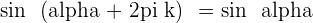
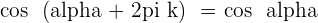

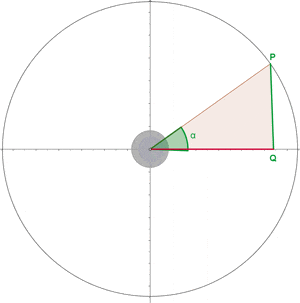

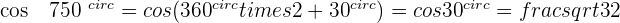
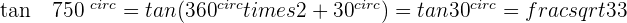
Angles That Differ by 90° or π/2 Rad
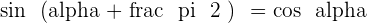
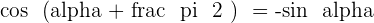
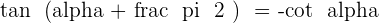

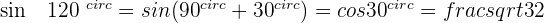


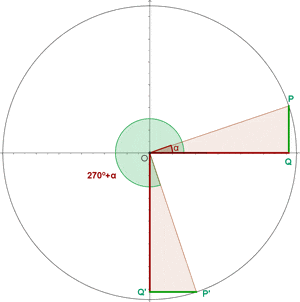
Angles That Add Up to 270º or 3/2 π Rad


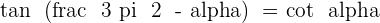
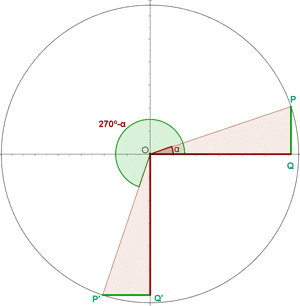
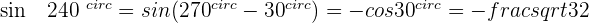
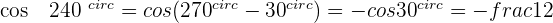
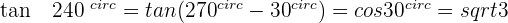
Angles That Differ by 270º or 3/2 π Rad


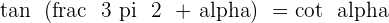

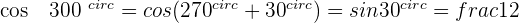
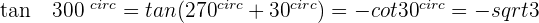













It was good and worth learning