Trigonometry domain is so wide that it extends to the real numbers. To show how these trigonometric ratios are inter-related, imagine a unit circle. The reason we call it a unit circle is because its radius is equal to  . Hence, the unit circle has its center at (0, 0) and its radius is one. The reason to draw the circle on the origin is to cut the circle into 4 different quadrants with the help of an axis. The x-axis is called abscissa and the y-axis is called ordinate. In the unit circle, the coordinate axes delimit four quadrants that are numbered in an anti-clockwise direction. Starting from
. Hence, the unit circle has its center at (0, 0) and its radius is one. The reason to draw the circle on the origin is to cut the circle into 4 different quadrants with the help of an axis. The x-axis is called abscissa and the y-axis is called ordinate. In the unit circle, the coordinate axes delimit four quadrants that are numbered in an anti-clockwise direction. Starting from 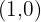 , the value of
, the value of 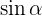 will be
will be  while the value of
while the value of 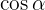 will be maximum because at
will be maximum because at 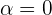 , the value of
, the value of 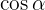 is maximum while the value of
is maximum while the value of 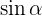 is minimum. As you move along the unit circle to the point P (shown in the diagram),
is minimum. As you move along the unit circle to the point P (shown in the diagram),  will have some value but we are not concerned about it right now, we are mainly concern about the entity of the value received from the trigonometric ratio, let's find whether we will get a positive or negative answer from the trigonometric ratios. Basically, we are drawing a triangle on the unit circle where straight lines, called line values, can be drawn whose length represents the value of a trigonometric function.
will have some value but we are not concerned about it right now, we are mainly concern about the entity of the value received from the trigonometric ratio, let's find whether we will get a positive or negative answer from the trigonometric ratios. Basically, we are drawing a triangle on the unit circle where straight lines, called line values, can be drawn whose length represents the value of a trigonometric function.

First Quadrant
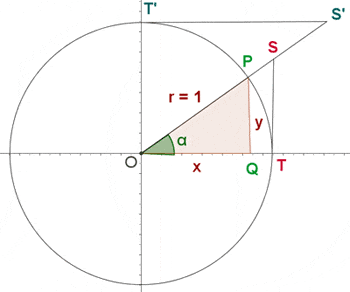
 , we know that
, we know that  since it is a unit circle.
since it is a unit circle.
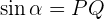
The line PQ is a straight line which is representing the value of ordinate. Since the line PQ is a positive line, we can conclude that the value of 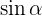 will always be positive in the first quadrant, let's find whether
will always be positive in the first quadrant, let's find whether 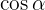 shows a similar result or not?
shows a similar result or not?

OQ is a line that is overlapping on the abscissa but what matters is whether it is overlapping on the positive abscissa or negative abscissa. Since we are talking about the first quadrant, all axes are positive, therefore, we can say that the value of 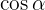 will always result positive in the first quadrant. In conclusion, the value of
will always result positive in the first quadrant. In conclusion, the value of 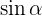 and
and 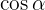 will always be positive in the first quadrant. Although,
will always be positive in the first quadrant. Although, 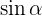 and
and 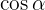 aren't the only trigonometric ratios, why don't you try to find other trigonometric ratios by yourself and let us know in the comments what did you find out?
aren't the only trigonometric ratios, why don't you try to find other trigonometric ratios by yourself and let us know in the comments what did you find out?
2nd Quadrant
Things are about to change because we are shifting towards the 2nd quadrant. In the second quadrant, the ordinate remained positive but the abscissa became negative, let's find whether this impacts the trigonometric ratios or not? Draw the same triangle of an angle  . Let's find the trigonometric ratios in the second quadrant.
. Let's find the trigonometric ratios in the second quadrant.
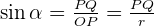
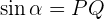
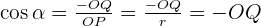
At this point, we know that the PQ line is positive but the line OQ is negative because it is overlapping on the negative x-axis hence the value of 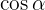 will be negative at any angle in the second quadrant. On the other hand, the value of
will be negative at any angle in the second quadrant. On the other hand, the value of 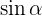 will remain positive at any angle in the second quadrant.
will remain positive at any angle in the second quadrant.
3rd Quadrant
In the third quadrant, both axes (abscissa and ordinate) are negative, we might see some changes in the trigonometric ratios, let's find out.
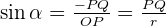

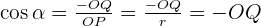
This time, the line PQ is a negative line, meaning the coordinates are negative (because of the negative y-axis) and the same goes for OQ, we can conclude that the value of 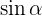 and
and 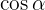 will always result negative for any angle in the third quadrant.
will always result negative for any angle in the third quadrant.
4th Quadrant
Finally, we move to the 4th quadrant where you will find negative ordinate and positive abscissa values.
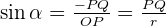


Finally, in this quadrant, the value of 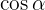 will be positive for any angle, however, the value of
will be positive for any angle, however, the value of 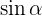 will be negative at any angle of the negative PQ line.
will be negative at any angle of the negative PQ line.
In Nutshell ...
The sine is the ordinate, that is to say, the y-coordinate or the vertical value in a pair of coordinates.
The cosine is the abscissa, that is to say, the x-coordinate or the horizontal value in a pair of coordinates.
From this data, the sign of the trigonometric ratios in each quadrant are as follows:
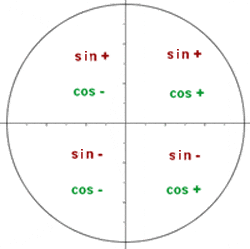
 |  |  | 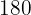 | 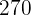 |
|---|---|---|---|---|
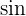 |  |  |  |  |
 |  |  |  |  |
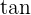 |  | 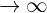 |  | 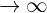 |













It was good and worth learning