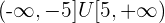Chapters
- Solve the Quadratic Inequalities
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10

The best Maths tutors available
Solve the Quadratic Inequalities
Exercise 1

Exercise 2
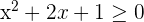
Exercise 3

Exercise 4
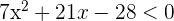
Exercise 5

Exercise 6

Exercise 7
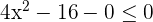
Exercise 8

Exercise 9
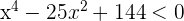
Exercise 10
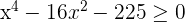
Solution of exercise 1

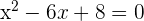
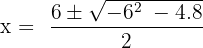
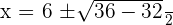
=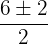


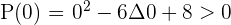
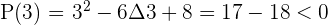
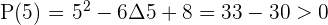

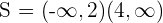
Solution of exercise 2
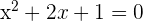
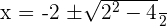



As a number squared is always positive.
S = 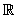
Solution of exercise 3





The sign obtained coincides with the inequality, the solution is 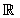
Solution of exercise 4
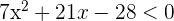
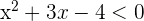

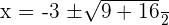
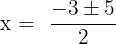
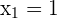
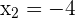
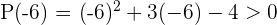
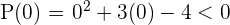
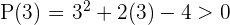

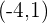
Solution of exercise 5



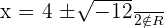

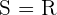
Solution of exercise 6

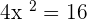
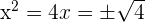
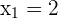
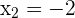



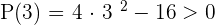

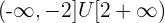
Solution of exercise 7
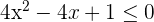

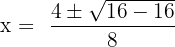
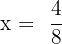
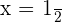
Solution of exercise 8
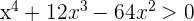

The first factor is always positive.


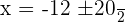

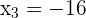


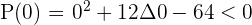
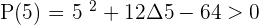


Solution of exercise 9

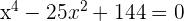
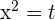
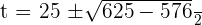


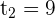

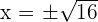

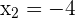
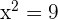
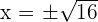

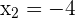

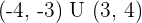
Solution of exercise 10

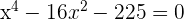
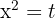


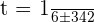
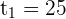
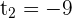

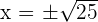

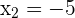
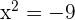
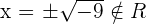
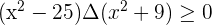
The second factor is always positive and different to 0.