Chapters
We already know how to solve linear equations in one and two variables. Now, it is time to learn how to graph linear inequalities in one and two variables on a number line and coordinate axis. The relationship between variables in linear inequalities is represented by four inequality symbols. These inequality signs are:
- < Less than
- < Greater than
 Less than or equal to
Less than or equal to Greater than or equal to
Greater than or equal to
We know how signs of the inequalities flip when we multiply them by a negative number. When we say that  then it means that c is strictly "greater" than d. The same goes for
then it means that c is strictly "greater" than d. The same goes for  , only "greater than" will be replaced by the "less than" word. When we say
, only "greater than" will be replaced by the "less than" word. When we say 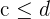 , then it means that c is either "less than or equal to d". The same goes for
, then it means that c is either "less than or equal to d". The same goes for  , only "less than" will be replaced by the "greater than".
, only "less than" will be replaced by the "greater than".
 means d is on the right side and c is on the left side of the number line. For example,
means d is on the right side and c is on the left side of the number line. For example,  is a true solution for the inequality
is a true solution for the inequality  . If you say that
. If you say that 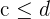 then
then  and
and 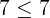 both are true solutions.
both are true solutions.
The above examples were related to simple linear inequalities. However, sometimes you are also given double inequalities, in which the inequality sign comes two times. For example, consider the following problem:
Write the following inequalities in the form of double inequality.
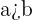 and
and 
Before solving, we know that a, b and c are interconnected. We can simply write them as a single inequality by seeing which expression is repeated. "a" comes two times in the above example, so we will place it in the middle. Since b is lesser than a, so it will be positioned first and c will be at third position.
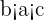
Let's see another example below.
 and
and 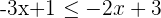
Now, first, consider which algebraic expression is repeated.  comes two times in the above example, so it will be positioned in the middle of the double inequality. The final inequality will look like this:
comes two times in the above example, so it will be positioned in the middle of the double inequality. The final inequality will look like this:


Linear Inequality in One Variable
Linear equations in one variable contain a single variable only. We can donate linear inequality in one variable in interval as well as set builder notation. In interval notation, we either use parentheses or square brackets depending on the beginning and endpoint of the interval. While denoting a closed interval in interval notation, we use square brackets on both sides because both points are part of the solution set. The graph of the linear inequality is represented on a number line.
We will solve some of the examples of linear inequalities in one variable and write them in interval notation. We will also represent them on a number line.
Example 1
Solve the inequality  .
.
Solution
First, we will multiply the constant 2 with the expression 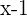 inside the brackets on the right hand side of the inequality:
inside the brackets on the right hand side of the inequality:
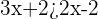
Now, subtract 2x from both sides of the inequality to get:
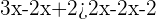
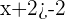
Again subtracting 2 from sides of the inequality will yield:


Hence, the final solution is  . It can be written in the interval notation as:
. It can be written in the interval notation as:

You can see that the beginning and endpoints are not part of the solution set, so we have used parenthesis on both sides in the interval notation and open circle on -4 on the number line. The inequality on the number line will look like this:

Example 2
Solve the inequality 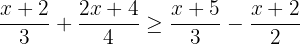 . Write the solution set in interval notation and represent it on a number line.
. Write the solution set in interval notation and represent it on a number line.
Solution
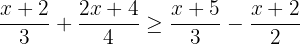
Take L.C.M of 3 and 4 on the left hand side, and 3 and 2 on the right hand side of the inequality:
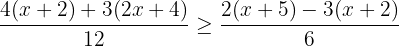
Multiplying the terms inside the brackets with constants will result in the following expression:
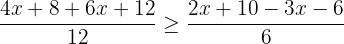
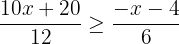
Cross multiply the denominators with the expressions in the numerator on both sides of inequality:
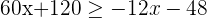
Adding 12x and subtracting 120 from both sides will give:

Divide both sides by 72 to get the following answer:

In the interval notation, we will write the answer like this:

As the final answer  means
means  is greater than or equal to -1, so -1 is included in the interval. We have used a square bracket before -1 in the interval notation and filled circle on the number line to indicate that. On a number line the solution will look like this:
is greater than or equal to -1, so -1 is included in the interval. We have used a square bracket before -1 in the interval notation and filled circle on the number line to indicate that. On a number line the solution will look like this:

Find various Maths tutor on Superprof.
Linear Inequality in Two Variables
So far, we have discussed how to solve linear inequality in one variable. In this section, we will discuss linear inequality in two variables. Linear inequality in two variables involves two variables instead of one. They are solved in the same way as the linear equations in two variables. Linear inequalities in two variables are represented like this:

When the values of  and
and  are substituted in the inequality, the final answer is a true statement. The solution of linear inequalities in two variables is represented as an ordered pair
are substituted in the inequality, the final answer is a true statement. The solution of linear inequalities in two variables is represented as an ordered pair 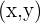 .
.
Example 1
Does the ordered pair 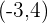 satisfy the inequality
satisfy the inequality  ?
?
Solution
To answer the question in this example, we will substitute the values in the ordered pair in the inequality. According to the question,  and
and 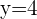 .
.
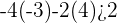
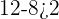
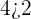
Hence, the ordered pair 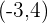 is the true solution to the inequality
is the true solution to the inequality  .
.
Example 2
Does the ordered pair  satisfies the inequality
satisfies the inequality 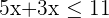 ?
?
Solution
To answer this question, substitute the values from the ordered pair in the inequality 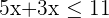 .
.
In the ordered pair 
 and
and 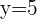 .
.
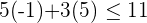


Hence, the ordered pair  satisfies the inequality
satisfies the inequality 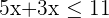 .
.
Find exceptional maths tutors near me.
Graphing Linear Inequalities in Two Variables
We know that when linear equations are plotted in an xy plane, the graph is a straight line. The graph of linear inequalities is also a straight line, but it divides the coordinate plane into two parts. One part of the plane which is mostly shaded represents the inequality. Let us learn how to graph linear inequalities in a coordinate plane through the following examples.
Example 1
Graph the inequality 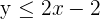 .
.
Solution
To graph the above inequality, first, we will construct a table as we do before graphing linear equations.
| x | y |
|---|---|
| -2 | -6 |
| -1 | -4 |
| 0 | -2 |
| 1 | 0 |
| 2 | 2 |
| 3 | 4 |
Using the points on the table plot a graph and shade the region below the line because the inequality has less than equal to sign.

Example 2
Solve the inequality  .
.
Solution
Simplify the inequality before constructing a table. Subtract 5 from both sides of the inequality to get the following expression:
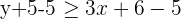

Now, construct a table of the above linear inequality like this:
| x | y |
|---|---|
| -2 | -5 |
| -1 | -2 |
| 0 | 1 |
| 1 | 4 |
| 2 | 7 |
| 3 | 10 |
Using the values of  and
and  from the table, plot the graph in the coordinate axis and highlight the region above the line because there is greater than equal to sign.
from the table, plot the graph in the coordinate axis and highlight the region above the line because there is greater than equal to sign.
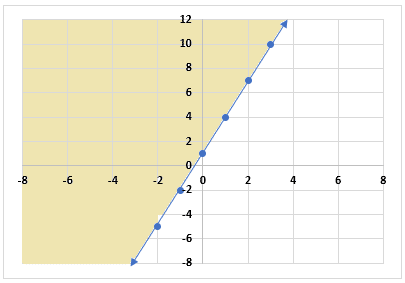
The shaded region above the line represents a solution of the inequality.
So far, we have learned how to plot the graphs of the inequalities which have  and
and  signs. Inequalities involving
signs. Inequalities involving  and
and  signs are plotted using a solid straight line. On the other hand, the inequalities which involve "<" or ">" sign are plotted using a dotted or dashed straight line because these are strict inequalities.
signs are plotted using a solid straight line. On the other hand, the inequalities which involve "<" or ">" sign are plotted using a dotted or dashed straight line because these are strict inequalities.
Now, we will see how to plot the graphs when the inequality has a "<" or ">" sign.
Example 3
Graph the inequality 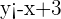 .
.
Solution
Before graphing, construct a table with the points  and
and  .
.
| x | y |
|---|---|
| -2 | 5 |
| -1 | 4 |
| 0 | 3 |
| 1 | 2 |
| 2 | 1 |
| 3 | 0 |
Using the points from the table, plot the graph of the inequality like this:
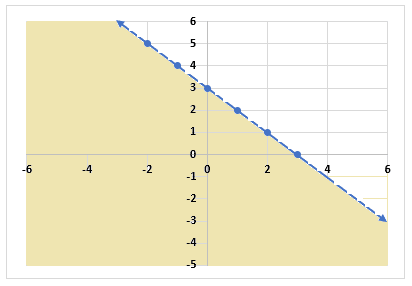
You can see that the dotted line is used to represent the straight line and the region below the dotted line is shaded.
Example 4
Graph the inequality  .
.
Solution
To construct the table, first solve the inequality by applying simple arithmetic operations.
Subtracting 9 from both sides of the inequality will give:

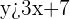
Construct the table of the inequality 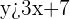 like this:
like this:
| x | y |
|---|---|
| -2 | 1 |
| -1 | 4 |
| 0 | 7 |
| 1 | 10 |
| 2 | 13 |
| 3 | 16 |
Using the above table, construct a graph like this:

As the inequality was strict, i.e. it has greater than sign, therefore we used a dotted straight line to represent it.
Check for an outstanding maths tutor near me here.
Check for the best Maths tutors on Superprof.













