June 26, 2019
x² − 6x + 8 > 0
It can be solved by following these steps:
1.Equal the polynomial of the first member to zero and the roots of the quadratic equation are obtained.
x² − 6x + 8 = 0
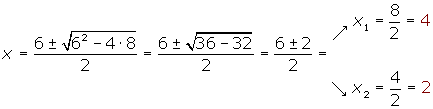
2. Represent these values in the real line. Take one point of each interval and evaluate the sign in each:
P(0) = 0² − 6 · 0 + 8 > 0
P(3) = 3² − 6 · 3 + 8 = 17 − 18 < 0
P(5) = 5² − 6 · 5 + 8 = 33 − 30 > 0
3. The solution is defined by the intervals (or the interval) that have the same sign as the polynomial.
S = (-∞, 2) ∪ (4, ∞)
x² + 2x +1 ≥ 0
x² + 2x +1 = 0
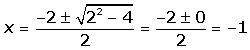
(x + 1)² ≥ 0
As a number squared is always positive the solution is 
.
| Solution | ||
|---|---|---|
| x² + 2x +1 ≥ 0 | (x + 1)² ≥ 0 |  |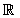
| x² + 2x +1 > 0 | (x + 1)² > 0 |  |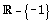
| x² + 2x +1 ≤ 0 | (x + 1)² ≤ 0 | x = − 1 |
| x² + 2x +1 < 0 | (x + 1)² < 0 |  |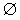
x² + x +1 > 0
x² + x +1 = 0
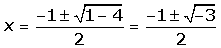
When there are no real roots, give the polynomial any value if:
The sign obtained coincides with the inequality, the solution is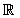 
.
The obtained sign does not coincide with that of the inequality and thus, has no solution.
| Solution | |
|---|---|
| x² + x +1 ≥ 0 |  |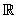
| x² + x +1 > 0 |  |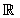
| x² + x +1 ≤ 0 |  |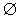
| x² + x +1 < 0 |  |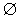
Example 1
7x² + 21x − 28 < 0
x² +3x − 4 < 0
x² +3x − 4 = 0
P(−6) = (−6)² +3 · (−6)− 4 > 0
P(0) = 0² +3 · 0 − 4 < 0
P(3) = 3² +3 · 3 − 4 > 0
(−4, 1)
Example 2
−x² + 4x − 7 < 0
x² − 4x + 7 = 0
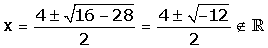
P(0) = −0² + 4 ·0 − 7 < 0
S =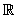 
Example 3
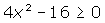
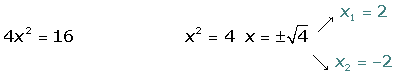
P(−3) = 4 · (−3)² − 16 > 0
P(0) = 4 · 0 ² − 16 < 0
P(3) = 4 · 3 ² − 16 > 0
(-∞, −2] ∪ [2, +∞)
Check for the best Maths tutors on Superprof.
Check for outstanding maths tutors near me here.
Get information about maths tuition in the UK.
Did you like the article?
Loading...