Chapters
Rational inequalities are represented by the following algebraic expression:
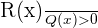
Here, the denominator  . The process of solving rational inequalities is the same as solving rational equations. Besides greater than inequality sign
. The process of solving rational inequalities is the same as solving rational equations. Besides greater than inequality sign 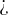 , other inequality symbols such as smaller than
, other inequality symbols such as smaller than 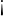 , greater than equal to
, greater than equal to  and less than equal to
and less than equal to  can also be used to depict rational inequalities.
can also be used to depict rational inequalities.
Unlike polynomial inequalities, rational inequalities involve denominators that is why they require extra caution. Rational inequalities are solved by finding the zeros or roots of the numerator and denominator. The zeros are also known as critical values. Like linear inequalities, if you want to flip the sign of the rational inequality, multiply both sides by a negative number.

Steps for Writing the Rational Inequalities in Interval Notation
Writing simple, compound and double inequalities in the interval notation are straightforward. Since, rational inequalities involve denominator too, therefore, writing them in the interval notation is tricky. Remember that we use parentheses or square brackets to write the equations or inequalities in interval notation.
In this article, we will see how to represent the solution set of rational inequalities in the interval notation and represent them on the number line. For this, we need to follow certain steps before writing the solution sets in the interval notation. These steps are explained below:
Step 1
For solving rational inequality, simplify it using simple arithmetic operations and find the zeros or roots of the numerator and denominator.
Step 2:
Using these roots, divide the number line into more than one intervals.
Step 3
Take points from each interval and substitute them in the inequality to check whether the points satisfy the inequality or not. It is recommended to construct a table like shown in the examples below.
Step 4:
Using the table from step 3, write the inequality in the interval notation and represent it on the number line.
The following examples show how to solve rational inequalities and express them in interval notation.
Get information about maths tuition in the UK.
Example 1
Solve the inequality 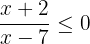 . Write the solution set in the interval notation and represent it on the number line.
. Write the solution set in the interval notation and represent it on the number line.
Solution
 and
and 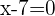
Isolate  on left hand side of the expressions by subtracting and adding constants on both sides of the equation.
on left hand side of the expressions by subtracting and adding constants on both sides of the equation.
 and
and 
We know that the denominator should be nonzero, so 7 is not part of the solution. The only solution we get is  which sets the inequality to 0. The inequality is less than or equal to zero, so there are other numbers too that will be the part of the solution set. Using the roots, we will divide the number line into three intervals:
which sets the inequality to 0. The inequality is less than or equal to zero, so there are other numbers too that will be the part of the solution set. Using the roots, we will divide the number line into three intervals:
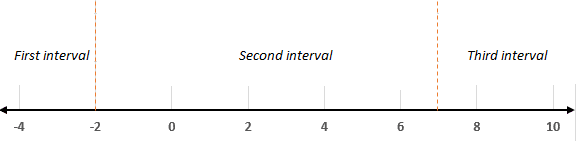
We will take some points from each of the above interval and substitute them in the inequality.
| x=-3 | x=-2 | x=0 | x=3 | x=7 | |
|---|---|---|---|---|---|
| >0 | 0 | <0 | <0 | Undefined | |
| Satisfies or Not satisfies | Not satisfies | Satisfies | Satisfies | Satisfies | Undefined |
We can conclude the following points from the above table:
- We can see in the table that the numbers which are less than -2, i.e. -3 are not true for the inequality
 . Thus, we can say that all numbers in the first interval except -2 do not satisfy the inequality.
. Thus, we can say that all numbers in the first interval except -2 do not satisfy the inequality. - The values which are greater than -2, like 0 and 3 are part of the solution. It means that all numbers in second interval satisfy the inequality.
- We cannot include 7 because it sets the denominator equal to 0 which makes the inequality undefined.
- -2 also satisfies the inequality. In other words, we can say that all numbers between -2 and 7 are part of the solution except 7.
Hence, before writing the inequality in the interval notation we will consider all of the above points. Since -2 is included, so we will use square bracket [ before -2 and 7 is not included, so ) will be used. The interval notation of the inequality 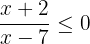 is
is  .
.
On a number line, the solution set of the inequality will look like this:
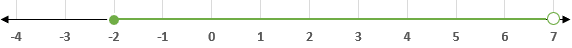
Example 2
Solve the inequality  . Write the solution set in the interval notation and represent it on the number line.
. Write the solution set in the interval notation and represent it on the number line.
Solution

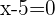 and
and 
 and
and 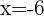
We know that the denominator cannot be equal to 0, so 6 is not included in the solution set. Using the above points, we will divide the number line into the following three intervals.

By substituting some points from the above intervals in the inequality we get the following results:
| x=-8 | x=-6 | x=0 | x=5 | x=6 | x=8 | |
|---|---|---|---|---|---|---|
| >0 | Undefined | <0 | 0 | >0 | >0 | |
| Satisfies or not satisfies | Not satisfies | Undefined | Satisfies | Not satisfies | Not satisfies | Not satisfies |
We can conclude the following points from the above table:
- The values lesser than or equal to -6, either do not satisfy the inequality or their result cannot be determined.
- Similarly, the values greater than equal to greater than 5 do not satisfy the inequality.
- The only value satisfying the inequality is lying between -6 and 5.
Hence, the interval notation of inequality is an open interval  written inside parenthesis. It shows that -6 and 5 are not part of the solution. Here, -6 is the beginning of the interval and 5 is the end point.
written inside parenthesis. It shows that -6 and 5 are not part of the solution. Here, -6 is the beginning of the interval and 5 is the end point.

Example 3
Solve the inequality 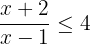 . Write the solution set in the interval notation and represent it on the number line.
. Write the solution set in the interval notation and represent it on the number line.
Solution
For simplifying, we need to subtract 4 from both right hand and left hand sides of the inequality to yield following algebraic expression:
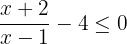
Combine both expressions by reducing into a common denominator:
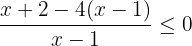
Multiplying -4 by the term 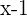 inside the brackets, we will get the following algebraic expressions:
inside the brackets, we will get the following algebraic expressions:
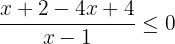
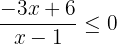
Now, find the roots of the numerator and denominator.
 and
and 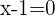
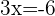 and
and 
 and
and 
We know that the denominator cannot be equal to zero, so we will exclude 1 from the interval. Using the above roots we will divide the number line into these intervals:
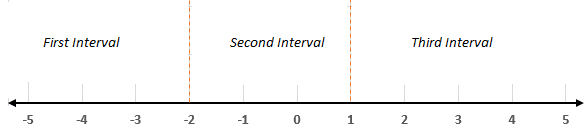
To write the solution set in the interval notation, we will substitute values from each of the above interval in the inequality and see their results in the form of the table.
| x=-3 | x=-2 | x=0 | x=1 | x=3 | |
|---|---|---|---|---|---|
| <4 | <4 | <4 | Undefined | <4 | |
| Satisfies or not satisfies | Satisfies | Satisfies | Satisfies | Undefined | Satisfies |
We can conclude the following points from the above table:
- All numbers which are less than or equal to zero satisfy the inequality. It shows that all numbers in the first and second intervals hold true for the inequality except 1. This situation can be described as

- Points above 1 also satisfy the inequality which shows that all numbers in the third interval except 1 are true for the inequality. This can be written as
 .
. - To write the inequality in interval notation, we just need to exclude 1 from the interval. In other words, we can say that the solution set is from negative infinity to positive infinity except the number 1.
To exclude 1 from the interval, we will write the solution set in union form. The interval notation of the inequality will be:
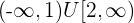
You can see that we wanted to exclude 1 but include the next number 2, so we used the brackets accordingly.
On the number line, this inequality will look like this:

So far we have solved problems involving single power variable. Now, we will see how to solve a quadratic inequality.
Example 4
Solve the inequality 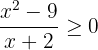 . Write the solution set in the interval notation and represent it on the number line.
. Write the solution set in the interval notation and represent it on the number line.
Solution
Simplify the quadratic inequality 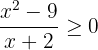 by factoring. The resulting equation will be:
by factoring. The resulting equation will be:
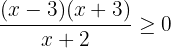 .
.
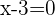 ,
,  and
and 
 ,
,  and
and 
The denominator cannot be equal to 0, so -2 is not part of the solution. Using the above roots we will divide the number line into these intervals as shown below: [Remember that, unlike linear functions, quadratics are represented by a parabola].

To write the solution set in the interval notation, we will take points from each of the above interval and see their results in the form of a table.
| x=-4 | x=-3 | x=-2 | x=0 | x=3 | x=4 | |
|---|---|---|---|---|---|---|
| <0 | 0 | Undefined | <0 | 0 | >0 | |
| Satisfies or not satisfies | Not satisfies | Satisfies | Undefined | Not satisfies | Satisfies | Satisfies |
We can conclude the following points from the above table:
- Value -4 does not satisfy the inequality, which shows that all the points in the first interval do not satisfy the inequality.
- -3 satisfies but -2 makes the inequality undefined. Hence, these points are expressed as
 .
. - 0 does not satisfy, so all numbers in the third interval are excluded from the solution set except 3.
- 3 and 4 in the fourth interval satisfy the equation which shows all numbers above 3 are included in the solution set. This can be expressed as
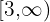 .
.
We will express the final result through a union of two sets described above. The interval notation will be:
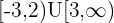
We will express the inequality on the number line like this:

Check for the best Maths tutors on Superprof.
Check for an outstanding maths tutor near me here.













