Chapters

What are Linear Inequalities
 " or less than equal to "
" or less than equal to " ". Linear inequalities with one variable contain a single variable only. Unlike the solution set of a linear equation in two variables which is given in ordered pair that satisfies both inequalities, linear inequality with one variable is given in interval notation.
". Linear inequalities with one variable contain a single variable only. Unlike the solution set of a linear equation in two variables which is given in ordered pair that satisfies both inequalities, linear inequality with one variable is given in interval notation. System of Linear Inequalities
We write systems of linear inequalities just like systems of equations using a curly bracket "{". The general startegy for solving inequalities is same as solving equations, however, the solution set of a system of inequalities is represented in a different way than the system of linear equations. Each linear inequality is solved separately and their solution sets are united to give the final solution of the entire system. The solution set is written either in parenthesis or square brackets. In this article, we will see how to solve the system of linear inequalities, write their solutions in interval notation and represent the solutions on the number line.
Find exceptional maths tutors near me.
Example 1
Solve the following system of linear inequalities with one variable. Write the solution set in interval notation and represent the system on a number line.
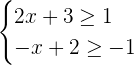
Solution
To find the solution set, we will solve the above inequality in multiple steps.
Step 1-Solving the inequalities in the system separately
The first inequality is 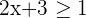 . Solve it algebraically like you solve linear equation.
. Solve it algebraically like you solve linear equation.
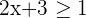
Subtraction of 3 from both sides of the inequality will give the following expression:
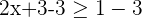

To isolate  on the left hand side of the inequality, both sides of the inequality will be divided by 2.
on the left hand side of the inequality, both sides of the inequality will be divided by 2.

In words, we can express this inequality as  is greater than or equal to -1. Let us solve the second inequality of the system now.
is greater than or equal to -1. Let us solve the second inequality of the system now.

Subtract -2 from both sides of the inequality to get the following expression:


Now, do you remember the rule of the inequality which says that if both sides of the inequality are multiplied by negative numbers, the sign of the inequality is reversed. Since the variable  has a negative sign associated with it, so multiplying both sides of the inequality by -1 will give the following result:
has a negative sign associated with it, so multiplying both sides of the inequality by -1 will give the following result:

We can see the multiplication of both sides by negative 1 has flipped the sign of inequality to less than or equal to.
Step 2 - Writing the solution set of both the inequalities in interval notation separately
Before writing the system of linear inequalities in interval notation, first, write each inequality in interval notation separately. After simplifying the first inequality 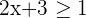 we got
we got  . In interval notation it will be written as:
. In interval notation it will be written as:

The simplified form of the second inequality  was
was  . In interval notation it will be written as:
. In interval notation it will be written as:

Step 3- Combining the solution set in interval notation of both inequalities
Now, we will unite the solution set of both the inequalities. The solution sets of both the inequalities are  and
and  . We will unite these like this:
. We will unite these like this:
 U
U 
Now, we will take the smallest beginning point and largest endpoint from both the intervals. The smallest beginning point is -1 and the largest endpoint is 3, so in interval notation, the final solution will be written as:

You can see that we have used square brackets on both sides of the beginning and endpoint because -1 and 3 were part of the solution set. It also shows that  is a closed interval.
is a closed interval.
Step 4-Representing the solution set on the number line
Now, the final step is to represent the solution set on the number line. You can either directly represent the solution set on the number line, or first, represent both inequalities separately as shown below. You can see that we have used closed circles for -1 and 3 because these two numbers were part of the solution set.

Example 2
Solve the following system of linear inequalities in one variable. Write the solution set in interval notation and represent the system on a number line.
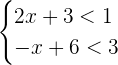
Solution
Like example 1, we will solve the above inequality in multiple steps.
Step 1-Solving the inequalities in the system separately
First, solve the first inequality in the system like this:
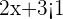
By subtracting 3 from both sides of the inequality we will get the following expression:

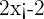
To isolate the variable  on the left-hand side of the inequality, divide both sides by 2:
on the left-hand side of the inequality, divide both sides by 2:

Now, solve the second part of the inequality 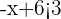
Subtract 6 from both sides of the inequality:

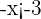
Since, the variable in the resulting inequality 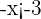 is negative, therefore we will multiply both sides by -1. This will also flip the inequality sign and change the sign of -3 on the right hand side.
is negative, therefore we will multiply both sides by -1. This will also flip the inequality sign and change the sign of -3 on the right hand side.
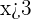
Step 2 - Writing the solution set of both the inequalities in interval notation separately
After simplifying the first inequality 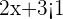 , we got
, we got  . In interval notation, it will be written as:
. In interval notation, it will be written as:

You can see that we have used parentheses on both sides of the inequality because -1 is not part of the solution.
The simplified form of the second inequality 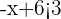 was
was 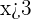 . In interval notation, it will be written as:
. In interval notation, it will be written as:

Again we have not used square brackets before or after beginning and endpoints because 3 is not included in the solution set.
Step 3- Combining the solution set in interval notation of both inequalities
Now, we will combine the solution set in interval notation of both the inequalities. The interval notation of the first inequality is  and the solution set in interval notation of the second inequality is
and the solution set in interval notation of the second inequality is  .
.
Uniting these inequalities gives us no solution at all.
Step 4-Representing the solution set on the number line
Since the system of inequality has no solution at all, so on the number line there will no common values represented which are part of both the inequalities.

Find various Maths tutor on Superprof.
Example 3
Solve the following system of linear inequalities with one variable. Write the solution set in interval notation and represent the system on a number line.
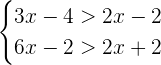
Solution
To find the solution set, we will solve the above inequality in multiple steps.
Step 1-Solving the inequalities in the system separately
First, solve the first inequality in the system like this:
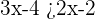
Apply basic operations of addition and subtraction to simplify the above inequality:
Adding 4 to both sides of the inequality will give:
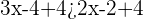
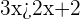
Subtract  from both sides of the inequality to isolate the variable
from both sides of the inequality to isolate the variable  on the left hand side:
on the left hand side:

Now, for solving the second part of the inequality 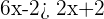 , combine the like terms like you do while solving linear equations:
, combine the like terms like you do while solving linear equations:
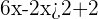

Divide both sides by 4 to get the resultant inequality in simplified form:

Step 2 - Writing the solution set of both the inequalities in interval notation separately
Simplifying the first inequality 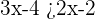 gave us
gave us  . The interval notation of the first inequality will be written like this:
. The interval notation of the first inequality will be written like this:

Similarly, by simplifying the second inequality 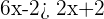 we got
we got  . The interval notation of the second inequality will be written like this:
. The interval notation of the second inequality will be written like this:

Step 3- Combining the solution set in interval notation of both inequalities
Now, we will combine the solution set in interval notation of both the inequalities. The interval notation of the first inequality is  and the solution set in interval notation of the second inequality is
and the solution set in interval notation of the second inequality is  . Unite these two inequalities like this:
. Unite these two inequalities like this:
 U
U 
The final solution set in interval notation will be written by taking the smaller beginning point and larger endpoints from the intervals of both inequalities. Since the smaller beginning point is 1 and the greater endpoint is  , so the interval notation of the system will be:
, so the interval notation of the system will be:

The final solution is an open interval.
Step 4-Representing the solution set on the number line
The interval notation of the system of inequalities is  . It shows that the interval has infinitely many solutions. On the number line, it will look like this:
. It shows that the interval has infinitely many solutions. On the number line, it will look like this:
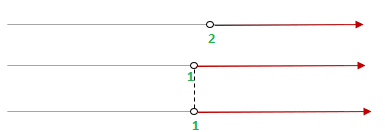
You can see that since 1 is not included in the interval, so we have used the open circle to represent it on the number line.
Example 4
Solve the following system of linear inequalities with one variable. Write the solution set in interval notation and represent the system on a number line.

Solution
Follow the following steps to solve the above inequality.
Step 1-Solving the inequalities in the system separately
Take the first inequality from the system and combine like terms by taking coefficients on the left hand side and constants on the right hand side of the inequality:
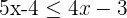
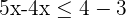

Now, solve the second inequality like this:

Subtract  and add 2 on both sides of the inequality:
and add 2 on both sides of the inequality:
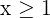
Step 2 - Writing the solution set of both the inequalities in interval notation separately
By simplifying the first inequality 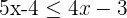 we get
we get  . The interval notation of the first inequality will be written like this:
. The interval notation of the first inequality will be written like this:
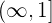
Similarly, by simplifying the second inequality  we got
we got 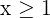 . The interval notation of the second inequality will be written like this:
. The interval notation of the second inequality will be written like this:
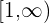
Step 3- Combining the solution set in interval notation of both inequalities
Now, we will combine the solution set in interval notation of both the inequalities. The interval notation of the first inequality is 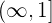 and the solution set in interval notation of the second inequality is
and the solution set in interval notation of the second inequality is 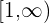 . Unite these two inequalities like this:
. Unite these two inequalities like this:
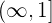 U
U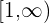
The final solution set in interval notation will be written by taking the smallest beginning point and largest endpoint from the intervals of both inequalities. Since the smallest beginning point is 1 and the greater endpoint is also 1, so the interval notation of the system will be:
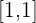
Hence, the system has only one solution. We have enclosed the only solution is square brackets because the interval is closed.
Step 4-Representing the solution set on the number line
The interval notation of the system of inequalities is 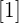 . It shows that the interval has only one solution. On the number line, it will look like this:
. It shows that the interval has only one solution. On the number line, it will look like this:

You can see that since 1 is included in the interval, so we have used the closed circle to represent it on the number line.
Check for the best Maths tutors on Superprof.
Check for an outstanding maths tutor near me here.













