Chapters
| < | less than | 2x − 1 < 7 |
| ≤ | less than or equal to | 2x − 1 ≤ 7 |
| > | greater than | 2x − 1 > 7 |
| ≥ | greater than or equal to | 2x − 1 ≥ 7 |
The solution set of an inequality is the set of all values which satisfies the variable in the inequality. In this article, we will see how to solve simple, double and compound inequalities through examples. We will also see how to represent inequalities in the interval and set builder notation, and on a number line.

How to Solve Inequalities
The process of solving equations and inequalities is same, however, unlike linear equations, while solving linear inequalities we need to be careful regarding the sign. This is because multiplication and division of both sides of an inequality by a negative number reverses the inequality sign. This does not happen in linear equation because the equality sign is constant through out the problem. However, multiplying or dividing both sides by a positive number causes no change in the inequality sign.
Find the best Maths tutor on Superprof.
Consider the following example:
Example 1
Solve the inequality 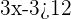 .
.
Solution
First of all, add 3 to both sides of the inequality:
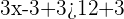
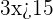
Divide by 3 to isolate  on the left side:
on the left side:
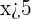
In other words, we can say that  can be any value greater than 5.
can be any value greater than 5.
Reversing the Inequality Signs
Sometimes, you need to flip the inequality sign. This happens when we multiply or divide both sides of the inequality by a negative number. Consider following examples:
Example 1
Solve the linear inequality 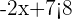
Solution
Subtract 7 from both sides of the inequality to get the following expression:

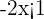
To isolate  on the left side of the inequality divide both sides by -2.
on the left side of the inequality divide both sides by -2.
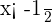
Since we have divided both sides of the inequality by a negative number, therefore the smaller than sign 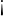 has changed to the greater than sign
has changed to the greater than sign 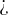 . Hence,
. Hence,  can be any value greater than
can be any value greater than 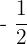 .
.
Example 2
Solve the inequality 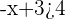
Solution
Subtract 3 from both sides of the inequality to get the following expression:
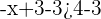
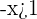
Divide both sides of the inequality by -1:

You can see that the sign of the final inequality has reversed because both sides of the inequality are divided by a negative number. Hence,  can be any value smaller than -1.
can be any value smaller than -1.
Example 3
Solve the inequality 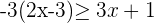 .
.
Solution
To simplify, the constant will be multiplied by term inside the brackets.

Subtract  from both sides of the inequality to get the following expression:
from both sides of the inequality to get the following expression:
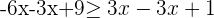
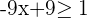
Subtract 9 from both sides of the inequality to get the following expression:
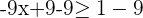

Divide both sides of the inequality by -9 to get the following result:
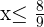
As you can see that both sides of the inequality were divided by a negative number, therefore the  is reversed to
is reversed to  . The final result shows that
. The final result shows that  can be any number less than or equal to
can be any number less than or equal to  .
.
Check for outstanding maths tutors near me here.
Solving Double Inequality
So far, we have solved expression with a single inequality sign. Sometimes, we are given a more complex expression in which there are two inequalities in a single expression.
In this part, we will see how to solve double inequality expressions through some examples.
Example 1
Solve the expression  .
.
Solution
To solve this expression, we will separately solve each part inequality and will combine the final answer. This problem will be solved in multi steps.
Step 1
First, we will solve  .
.
Add 3 to both sides of the inequality to get the following expression:
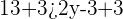

By simplifying the inequality by dividing both sides by 2 we will get the following answer:
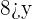 or
or 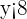
Step 2
Now, solve the second part of this inequality  .
.
Add 3 to both sides of the inequality to get the following expression:


Divide both sides of the expression by 2 to get the answer to this part of inequality:
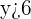
Step 3
Now, we will combine the answers of step 2 and step 3 into a single expression. The result of the first part was 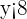 and the result of the second part was
and the result of the second part was 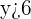 . We will combine both the results by placing
. We will combine both the results by placing  in the middle of the expression. Hence, the resultant expression will be:
in the middle of the expression. Hence, the resultant expression will be:
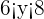
Solving Compound Inequalities
Compound inequalities are joined by OR or AND word. In this part, we will solve the examples of compound inequalities with OR or AND word.
Compound Inequality with OR Example
Solve the expression 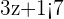 OR
OR  .
.
Solution
Solve both the inequalities separately. First, we will solve 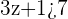 .
.
Subtract 1 from both sides of the inequality to get:
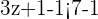
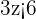
Divide both sides by 3 to get the result:
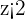
Now, solve the second part of the inequality  .
.
Divide both sides by 2 to get the result:
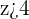
The final answer is either 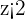 or
or 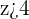 .
.
Compound Inequality with AND Example
Solve the expression  AND
AND  .
.
Solution
Solve both the expressions separately to get the final answer of this expression. First, we will solve  .
.
Subtract 5 from both sides of the inequality to get the following expression:
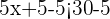
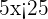
Divide both sides by 5 to get the final answer:
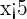
Now, solve the second part of the expression  .
.
Subtract 6 from both sides of the expression to get the final answer:
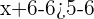

Hence, we have two results 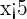 AND
AND  . We can further simplify it as:
. We can further simplify it as:

Using Interval Notation to express Inequalities
We can write inequalities in interval notation, but solving inequalities is essential before writing them in interval notation. Interval notation means writing inequality in parentheses or square brackets with just beginning and end numbers. Interval notation follows specific rules such as:
- If we do not want to include the numbers in the interval, then we use parenthesis on both sides ().
- If we want to include the numbers in the interval, then we use square brackets on both sides [].
- If first number, i.e. beginning of interval is part of the solution, but the end point isn't, then we enclose them in [ ) brackets.
- If the first number isn't the part of the solution, but the end point is, then we enclose the numbers in ( ].
These rules will be cleared through the examples in this part.
Closed Interval
If both the numbers are included in the interval, then we use square brackets on both sides. This shows that the interval contains all values between these two numbers including the numbers. This type of interval is known as closed interval.
Example 1
Write the inequality  in interval notation.
in interval notation.
Solution
Solve this inequality before writing in interval notation.
Add 1 to both the sides of the inequality to get the following expression:


Divide both sides by 3:

The result shows that  is any number greater than 2. To write it in the interval notation, we will use () brackets because 2 is not the part of solution. Hence, the interval notation of this inequality is:
is any number greater than 2. To write it in the interval notation, we will use () brackets because 2 is not the part of solution. Hence, the interval notation of this inequality is:

Example 2
Write the inequality  in interval notation.
in interval notation.
Solution
First, solve the inequality by subtracting 4 on both sides:


Divide both sides by 4 to get the following result:

The result shows that  can be any number greater than or equal to 2. This inequality is written in interval notation as:
can be any number greater than or equal to 2. This inequality is written in interval notation as:

As you can see in the above example that 2 was included in the interval, so we used square bracket "[" before 2. In other words, we can say that the solution extends from 2 to infinity.
Example 3
Write the inequality 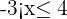 in interval notation.
in interval notation.
Solution
In this example, we have two inequalities in the same expression. We can simply write it in the interval notation by checking the signs of the inequality. The expression can be stated as  is any number greater than -3, but less than equal to 4. From the expression, we can conclude that -3 is not included in the interval, however, 4 is included because the sign
is any number greater than -3, but less than equal to 4. From the expression, we can conclude that -3 is not included in the interval, however, 4 is included because the sign  is used.
is used.
Hence, the interval notation of this inequality will be 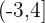 .
.
Get information about maths tuition in the UK.
Expressing Inequalities in Set Builder Notation
Besides interval notation, we can also write inequality in set builder notation. We write set builder notation using curly brackets {}. The following examples show how to write the inequalities in set builder notation.
Example 1
Write  in set builder notation.
in set builder notation.
Solution
{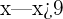 }
}
Sometimes, we are given a statement of inequality instead of mathematical expression. Consider the following example:
Example 2
 is an integer that is greater than equal to -6.
is an integer that is greater than equal to -6.
Solution
To write the above statement in set builder notation, we will first specify that  is an integer. We know that integers are represented by Z, so the set-builder notation will be:
is an integer. We know that integers are represented by Z, so the set-builder notation will be:
{ }
}
Example 3
 is a real number that is smaller than 4.
is a real number that is smaller than 4.
Solution
To write the above statement in set builder notation, we will first specify that  belongs to the set of real number. We know that real numbers are represented by R, so the set-builder notation will be:
belongs to the set of real number. We know that real numbers are represented by R, so the set-builder notation will be:
{ }
}
Graphing Inequalities
We can also graphically represent the inequalities on the number line. The following rules should be kept in mind while representing inequalities on a number line:
- If the number is not included in the interval, then we use an unfilled circle to represent it on the number line.
- If the number is included, then we use a filled circle to represent it on the number line.
Example 1
Represent 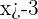 on a number line.
on a number line.
Solution
Since,  is greater than -3, so we will use an unfilled circle on -3 on a number line. It is better to write the inequality in interval notation first before representing it on a number line. The interval notation of
is greater than -3, so we will use an unfilled circle on -3 on a number line. It is better to write the inequality in interval notation first before representing it on a number line. The interval notation of 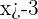 is
is  . The graph will look like this:
. The graph will look like this:

Example 2
Represent  on the number line.
on the number line.
Solution
This is an example of double inequality. The interval notation will be 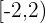 . The interval notation shows that the value of
. The interval notation shows that the value of  is all numbers between -2 and 2. Since -2 is included in the interval, so we will use square bracket "[" before it. The graph will look like this:
is all numbers between -2 and 2. Since -2 is included in the interval, so we will use square bracket "[" before it. The graph will look like this:

Example 3
In this example, we will graph compound inequality on a number line. Consider the following compound inequality with OR.
 OR
OR 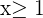
Solution
Since this inequality has two parts with OR sign, therefore its better to write the interval notations of both the inequalities first.
The interval notation of the expression  will be
will be  and of the expression
and of the expression 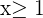 will be
will be 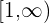 . Both the expressions will be graphed like this:
. Both the expressions will be graphed like this:

Learn more from Maths tutors near me on Superprof.













