Chapters

Decimal Numbers - An Introduction
Types of Decimal Numbers
There are two types of decimal numbers- terminating and non-terminating. Terminating decimals can be expressed as fractions, hence they are rational numbers. As the name suggests, these numbers have a finite number of digits after the decimal point.
Non- terminating decimals have an infinite number of digits at their decimal places. Non – terminating decimal numbers can be recurring or non-recurring. Recurring decimals are those decimal numbers in which the numbers in the decimal places are repeated in a specific order. On the other hand, non- recurring decimal numbers are those numbers in which the digits after the decimal point are not repeated in a specific order.
Conversion of Decimal Numbers
We can convert decimal numbers to fractions by eliminating the decimal point in the numerator and adding zeroes followed by a unit in the denominator. The number of zeroes are equal to the number of decimal places in the number. For example, 2.375 can be written in a fractional form like this:
= 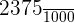
As there were 3 decimal places in the number 2.375, so we have converted it into the fractional form by adding 3 zeroes followed by 1 in the denominator.
We can also convert fractions to the decimal numbers. We consider the number of zeroes in the denominator and move the decimal point to the left. For example, consider the fraction 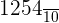 . As there is a single zero in the denominator, so we will move the decimal point one place to the left of the number in the numerator. Hence, this fraction is equal to the decimal number 125.4.
. As there is a single zero in the denominator, so we will move the decimal point one place to the left of the number in the numerator. Hence, this fraction is equal to the decimal number 125.4.
Adding or Subtracting Decimal Numbers
Like whole numbers, decimal numbers can be added, subtracted, multiplied and divided together. However, before proceeding to the addition, subtraction, and multiplication of the decimal numbers, one should know what the place values of the decimal numbers are.
The whole number part of the decimal number is arranged from right to left in a sequence units, tens, hundreds, thousands, ten-thousands and so on. The fractional part of the decimal number is arranged from left to right in a sequence tenths, hundredths, thousandths, ten – thousandths and so on.
The unit of the decimal number is added or subtracted from the unit of another decimal number. The same goes for the rest of the place values of the decimal numbers. You cannot add the digit at the tenths place of one decimal number to the digit at the hundredths place of another decimal number. Before performing the vertical addition or vertical subtraction of two or more decimal numbers, the individual digits are lined up in columns like this. The digits of the second number are placed in the exact sequence under the first number.
Thousands Hundreds Tens Units Tenths Hundredths Thousandths
Thousands Hundreds Tens Units Tenths Hundredths Thousandths
Example 1
Solve 121.564 + 24.340 + 1.25
Solution
Place the numbers in a column so that the decimals line-up. We will add (or subtract) units with units, tenths to tenths and hundredths to hundredths and so on.

Example 2
Add (or subtract) units with units, tenths to tenths, hundredths to hundredths...
342.528 + 6 726.34 + 5.3026 + 0.37 =?
Solution

Example 3
Solve 372.528 - 69.68452.
Solution
In this example, we will again line up hundreds with hundreds, tens with tens, units with units, tenths with tenths, hundredths with hundredths and so on.

Example 4
A cyclist has covered a distance of 12 kilometers 200 meters in the north direction and 25 kilometers and 550 meters in the south direction. How much distance has he covered altogether?
Solution
We need to find out the total distance covered by the cyclist. To do so, we need to add the distance covered in the north and south direction together. But before adding the distance, we will write the distance in suitable decimal numbers.
It is given that the cyclist has covered a distance of 12 kilometers and 200 meters in the north. We know that there are 1000 meters in a single kilometer, hence 100 meters represent 0.1 kilometers. With this logic, 200 meters are equal to 0.2 kilometers. It means that he has covered a 12.2 kilometers distance in the north direction. Using the same concept, we can say that the cyclist covered 25.55 kilometers in the south direction. We will find the total distance covered by him by adding these two distances like this:
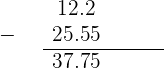
Hence, the total distance covered by him is 27.75 kilometers.
Example 5
Sarah's height is 5 feet 5 inches. Her younger brother is 3 feet 10 inches tall. How much taller is Sarah from her younger brother?
Solution
Well, to answer this question, we need to determine what is required in this question. We are given the heights of two people and are asked how much taller one person is than the other. It means that we need to subtract the height of Sarah's brother from Sarah's height.
To do so, we need to write the heights of both the siblings in the decimal form because their heights are given in 2 different units. If Sarah is 5 feet 5 inches tall, then it means that she is 5.5 feet tall. If Sarah's brother is 3 feet 10 inches tall, then it means that he is 3.10 feet tall. To subtract, line up both the decimal numbers in such a way that units are under units, tens are under tens, tenths are under tenths and so on.

Hence, Sarah is 2.4 feet taller than her younger brother.
Example 6
Solve 345.628 + 56.725 - 210.985
Solution
In this example, two different arithmetic operations addition and subtraction are used. We can solve this example, in two ways. First, we can subtract the third number from the second one and then add the resulting answer to the first number or we can add the first two numbers and then subtract the third number from the resulting answer obtained after the addition of the first two numbers.
Let us add the first and second number together like this:

Now, we will subtract the third number from the above answer like this:

Hence, the final answer is 191.368.













If it is (0.0072÷6)
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081