Chapters
Decimal numbers have two parts - a whole number part which is before the decimal point and a fractional part which has the digits after the decimal point. The fractional part of the decimal point is always less than one. A decimal point is a period or dot that segregates these two parts. As you move right to the fractional part of the decimal point, each place value decreases ten times. The fractional part of the decimal point are arranged from left to right in the following sequence:
Tenths Hundredths Thousandths Ten - thousandths ....
We can easily convert decimals to fractions and fractions to decimals. Decimal numbers are of two types - terminating and non - terminating decimal numbers. Non - terminating decimals are further divided into recurring or repeating decimals and non - recurring or non-repeating decimal numbers. In this article, we will see how to order and compare terminating decimal numbers.

Representation of Decimal Numbers on a Number Line
Each decimal number has a place in the numerical straight line. To represent the tenths, divide the unit into 10 parts.
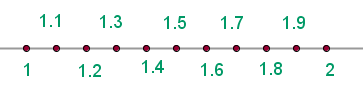
To represent the hundredths, divide each tenth into 10 parts.

To represent the thousandths, divide every hundredth into 10 parts, and this process continues for ten-thousandths, hundred-thousandths, ...
For example, consider the whole number 3. To represent a tenth of the number, we will divide 3 by 10. The resulting decimal number will be 0.3. 10 times 0.3 will be equal to 3. Similarly, to divide 3 into 100 equal parts divide it by 100. The answer will be 0.03 which shows that 100 times 0.03 will be equal to 3. You can also divide the whole number into 1000 equal parts by dividing it by 1000. The result will be 0.003.
Which part is greater, the tenth, hundredth or thousandth?
The answer is straightforward and simple. The tenth part is greater followed by a hundredth and then thousandth. We can arrange it in the ascending order like this:
0.003 < 0.03 <0.3
Similarly, in descending order, these values will be arranged like this:
0.3>0.03>0.003
There are no two consecutive decimal numbers because between two decimal numbers it is always possible to find other decimals.
Ordering Decimals
Ordering decimal numbers can be confusing. For example, if you are given two numbers 3.67 and 3.409 and are asked which number is greater, then you may answer 3.409 because it has more digits as compared to 3.67. But, this answer is wrong. The correct answer is that 3.67 is greater than the decimal number 3.409.
3.67 is greater because of the trailing zeros concept. Trailing zeroes are added to the right of the decimal number and do not affect the value of the decimal number. Therefore, we can write 3.67 as 3.670. You can make a place value chart by writing the place values of two decimal numbers lined up in columns like this:
Unit Decimal point Tenths Hundredths Thousandths
3 . 6 7 0
3 . 4 0 7
So, now it may have become easier for you to answer which is the greater number. This shows that you must have a number sense before solving the questions related to ordering or comparing decimals. Remember that if the decimal number is given without trailing zeroes and the other number has more digits, then you can add trailing zeroes to the number with fewer digits.
We can order the decimal numbers in the following two ways:
- Ascending : Smallest to the greatest
- Descending order : Greatest to the smallest
Now, we will see some of the examples related to ordering the decimal numbers.
Example 1
Order the following decimal numbers in descending order:
3.2 , 4.15, 3.36, 3.109, 3.45, 3.65
Solution
Descending order is the order of the numbers from the greatest to the smallest value. First, we should see the whole number part of the decimal numbers. The bigger the unit, ten, hundred or thousand of a number is, the greater is the number. In the above series of numbers, all units are 3 except 4.15. So, it is the greatest number.
Now, let us see the other numbers. The greater number of decimal places is up to a thousandths place, so we will add trailing zeroes to the numbers which have a lesser number of digits at their decimal places.
4.150, 3.650, 3.450, 3.360, 3,200, 3.109
Example 2
Arrange the following series of numbers in an ascending order:
0.5, 0.14, 0.9, 0.98, 0.81, 0.658, 0.783
Solution
Ascending order is the order of numbers from the smallest to the greatest value. To begin ordering the above series of numbers, we should see the whole number part of the decimal numbers first. The whole number part of all the decimal numbers is equal, i.e. 0.
The next step is to look at the decimal part of the numbers in the series. It is advised to add the trailing zeroes to the numbers which have a lesser number of digits at their decimal places. Hence, after adding the trailing zeros the series will look like this:
0.500, 0.140, 0.900, 0.980, 0.810, 0.658, 0.783
Now, it has become easier for you to arrange the above series in the ascending order like this:
0.14, 0.5, 0.658, 0.783, 0.81, 0.9, 0.980
Example 3
Arrange the following series of numbers in a descending order
6.67, 6.09, 7.001, 6.86, 6.05, 6.6, 6.7
Solution
First, look at the whole number parts of the above decimal numbers in the series. All numbers have 6 units except the number 7.001. Since, 7>6, therefore the number 7.001 is the greatest in the series. Add trailing zeroes to the other decimal numbers for the ease of ordering.
6.670, 6.900, 7.001, 6.860, 6.050, 6.600, 6.700
The descending order of the above series of numbers is given below:
7.001, 6.05, 6.6, 6.67, 6.7, 6.86, 6.9
Example 4
The heights of plants A, B, C, and D are given below in sequence. Which plant has a height greater than plant B, but less than plant D?
Plant A = 6.67 feet
Plant B = 6.09 feet
Plant C = 6.78
Plant D = 6.7
Solution
To answer the above question, we need to arrange the heights of the plants in either ascending or descending order.
The ascending order of the heights of the plants is given below:
6.09, 6.67, 6.7, 6.78
Or we can write it like this in ascending order:
B < A < D < C
The ascending order of the heights gives us an answer to this question. Plant A has a height greater than B, but less than D.
Example 5
The lengths of five rectangular boxes are given below. Which rectangular box has a length less than box C, but greater than box E.
Box A = 13.25
Box B = 14.02
Box C = 13.6
Box D = 13.49
Box E = 13. 3
Solution
We can arrange the above lengths in the descending order like this:
14.02, 13.6, 13.49, 13.3, 13.25
Alternatively, we can represent the heights ins descending order like this:
B > C > D > E > A
The above order shows that the box D has length lesser than box C, but greater than box E.
Example 5
The prices of 5 colored boxes of pencils in given below.
Blue = $9.87
Green = $9.02
Pink = $9.4
White = $9.61
Black = $9.1
Which colored box has price greater than Pink but less than Blue?
Solution
To answer this question, we must arrange the prices in ascending order like this:
9.02, 9.1, 9.4, 9.61, 9.87
We can write the sequence like this:
Green < Black < Pink < White < Blue
We can see that the white-colored pencil box has a price greater than pink but less than blue.
Find more Maths tuition here on Superprof.













If it is (0.0072÷6)
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081