Chapters

What is a Decimal Number?
A decimal number is a number that has a decimal point between the whole number and the fractional part. The point or dot which is used to segregate these two parts acts as a separator and is known as a decimal point. The numbers after the decimal point are smaller than 1.
For example, in the decimal numbers 12.328 and 3.656, 12 and 3 are whole numbers, whereas the numbers 328 and 656 following the decimal point are fractional part of the number. The fractional part of the decimal number is smaller than 1. In the above examples, the fractional parts of the numbers are 0.328 and 0.656.
The numbers after the decimal point are termed as tenths, hundredths, and thousandths. For example, if we have to write the number one hundred one and 9 tenths numerically, then we will write it as 101.9. Here, 101 is a whole number and 9 represents the fractional part.
Similarly, consider another example. Write 55, 6 tenths and 8 hundredths numerically. Here, 55 is a whole number, 6 is the first digit after the decimal point and 8 is the next digit after 6. Numerically, we can write it as 55.68.
Converting Decimals to Fractions
To express a decimal number as a decimal fraction, write the number without the decimal point as the numerator and as the denominator a 1, followed by as many zeros as there are decimal places in the decimal number. In other words, we can say that the denominator of a decimal fraction is the unit followed by zeros.
Examples
The following examples show how to converts decimals to fractions.
1. Write 0.3 in fractional form.
In place of the decimal point, we will use 1 in the denominator followed by zeroes. Since there is only one digit after the decimal point, therefore after 1 there will be only a single zero. The fractional form is:

2. Write 7.36 in fractional from.
The denominator will have one followed by 2 zeroes because there are two digits after the decimal point. The numerator will be the number without the decimal point.
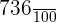
Converting Fractions to decimals
Now we will see how to convert fractions to decimals. See the following examples:
1. Convert 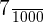 to a decimal number.
to a decimal number.
There are 3 zeroes after 1 in the denominator. First, we will write 7 as it is and put 2 zeros before it like this:
007
Next, we will put a decimal point on the left side of the first zero. The resultant decimal number is:
0.007
2. Convert 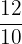 into a decimal number
into a decimal number
Since there is a single zero after 1, hence we will put a decimal point after 1. The resultant decimal number will be 1.2.
Decimal Units
They are fractions whose numerator is 1 and the denominator is a power of 10. Consider the following examples:
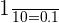 1 tenth
1 tenth
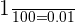 1 hundredth
1 hundredth
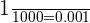 1 thousandth
1 thousandth
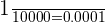 1 ten thousandth
1 ten thousandth
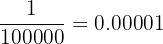 1 hundred thousandth
1 hundred thousandth
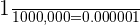 1 millionth
1 millionth
Place Values
Sometimes you are given a decimal number and asked about the place values of its digits. Remember that the digits of whole number part of a decimal number are sequenced from right to left and are termed as unit, tens, hundreds, thousands, ten thousands and so on.
Examples
1. 1456
In the above number, 6 is the unit, 5 is tens, 4 is hundreds and 1 is thousands.
2. 35678
In the above number, 8 is a unit, 7 is tens, 6 is hundreds, 5 is thousands and 3 is ten thousand.
The above two examples show how to write the values of the digits of the whole numbers. The case is different for the decimal part of the number. The numbers after the decimal point are sequenced from left to right and are termed as tenths, hundredths, thousandths, ten-thousandths and so on. Consider the following set of numbers in decimal format.
3. 34.619
In the above number, 32 is the whole number part and 619 is the decimal part of the number. The place value of all the digits is as follows:
The place value of 6 is tenths
The place value of 1 hundredths
The place value of 9 is thousands
The place value of 4 is units
The place value of 3 is tens
4. 157.543
In the above number, 157 is the whole number part and 543 is the decimal part of the number. We will start with the decimal part from left to right. The place values of all the digits are as follows:
The place value of 5 is tenths that is the first decimal place
The place value of 4 is hundredths
The place value of 3 is thousandths
Now, let us proceed to the whole number part.
The place value of 7 is units
The place value of 5 is tens
The place value of 1 is hundreds
Rounding Decimals
The process of rounding the decimals to the nearest integers is as follows:
- To round off the decimal number, you should know the place value up to which you want to round off the number.
- Once you know the place value, you should look at the digit of the decimal number at the right of that place value.
- If the decimal digit is smaller than 5, then write the previous decimal digit as it is.
- If the decimal digits are greater than or equal to 5, increase the previous decimal by one number.
You can be given the number of decimal places or the place values of decimal numbers in the questions which involve rounding. Your concepts about rounding numbers will be clarified through the following examples.
Examples
1. Round the decimal number 2.356478 up to two decimal places.
To round off the above number up to two decimal places, first, consider the third digit after the decimal point. The third digit is 6, therefore we will add 1 to the previous digit 5. The resulting number with two decimal places will be 2.36.
2. Round the decimal number 6.781456 up to four decimal places.
Since we need to round off the above number up to four decimal places, therefore we will see the fifth decimal digit. The fifth digit is 5, which means that we will increase the fourth digit by one unit. The resultant decimal number up to four decimal places is 6.7815.
3. Round the decimal number 8.9123 up to one decimal place.
One decimal place means that there should be one decimal digit after the decimal number. For rounding the above number, we will consider the second digit after the decimal point. The second decimal digit is 1, hence the resulting number up to one decimal place is 8.9.
4. Round up the decimal number 1.26123 to the nearest tenth.
Rounding the decimal number to the nearest tenth means that after the decimal point, there is a single digit. In other words, we can say that it means rounding the decimal number to one place. See the second digit after the decimal point of the above number. Since the second decimal digit is 6 which is greater than 5, therefore we increase the previous digit by one unit. The resulting number after rounding off will be 1.3.
5. Round the number 7.76543201 to the nearest hundredth.
Round to the nearest hundredth means that the decimal number should have 2 digits after the decimal point. To round off the number, see the third digit after the decimal point which is 5. The resultant number obtained after rounding up to two decimal places will be 7.77.
6. Round the number 1.34556 up to three decimal places.
Rounding the number up to three decimal places means that there should be three digits after the decimal point. To round off the above number up to three decimal places, look at the fourth digit after the decimal point. Since the fourth digit is 5, hence we will increase the last digit before the fourth one by one unit. The resultant number will be 1.346.
7. Round the decimal number 20.98138 up to three decimal places.
The fourth digit of the above number is 3 which is less than 5, hence we will write the number as it is, but up to 3 decimal places. The resulting number after rounding will be 20.9813.
Truncate Decimals
Truncating means to reduce the decimal part of the number up to a certain decimal place value without rounding. To truncate a decimal to a given order leave the figures prior to that order and eliminate the others.
Examples
The following examples show the truncated decimal numbers.
1. Truncate 2.3647 to the tenths place.
Truncation to tenths means that there should be a single digit after the decimal point. We will simply write the decimal number up to one decimal place as 2.3.
2. Truncate 2.3647 to the nearest hundredths.
After truncation to the nearest hundredths, we will get the number 2.36.
3. Truncate 2.3647 to the nearest thousandths.
After truncation to the nearest thousandths, we will get the number 2.364.
4. Truncate 2.3647 to the nearest ten thousandths.
After truncation, to the nearest ten-thousandths, we will get the number 2.3647.













If it is (0.0072÷6)
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081