Chapters
A decimal number has two parts _ a whole number and a fractional part. These two parts are separated by a period or dot, which is known as a decimal point. The fractional part of the decimal number is always considered less than 1.
Examples
69.356, 2.370 and 8.142 are examples of decimal numbers. You can see that there are two parts in these decimal numbers. One part is on the left side of the decimal, which is also known as a whole number part, whereas, the other part is on the right side of the decimal number which is also known as a fractional part.
Let us now consider the above decimals separately.
- 69.356: In this decimal number 69 is a whole number and 0.356 is a fractional part.
- 2.370: In this decimal number, 2 is a whole number, whereas 0.370 is a fractional part.
- 8.142: In this decimal number, 8 is a whole number, whereas 0.142 is a fractional part.
The digits in the whole number part of the decimal numbers are arranged from right to left in the sequence unit, ten, hundred, thousand, ten-thousand and so on. On the other hand, the fractional part of the decimal number is arranged from left to right in the sequence tenths, hundredths, thousandths, ten-thousandths and so on.
Types of Decimals
The two types of decimal numbers are explained below.
1. Terminating decimals
These decimal numbers have a finite number of digits after the decimal point. For example, 21.365, 6.234, 9.8 and 10. 2 are examples of terminating decimal numbers because the number of decimal places is countable. These decimal numbers can be expressed as fractions; hence they are the rational number. Remember that a rational number is a number that can be written in the form of p/q.
2. Non - terminating decimals
These decimal numbers have an infinite number of digits after the decimal point, i.e. the number of decimal places cannot be counted. There are further two types of non-terminating decimal numbers which are recurring and non-recurring decimals.
- Recurring decimals are repeating decimals. In other words, we can say that the digits in their decimal places are repeated endlessly in the same order. The examples of such decimal numbers include 1.3333... , 1.454545...., 3.324324324... and 2.454545.... Besides adding dots after these numbers, we can also express these numbers by adding a bar sign over them. For example, 1.333... can be written as
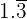 . Since we can express these decimals as fractions, hence they are rational numbers.
. Since we can express these decimals as fractions, hence they are rational numbers.
- Non-recurring decimals are non-repeating decimals. In non-recurring decimals, the digits in the decimal places are infinite but are not repeated in the same order. For example, the decimal numbers 1.35671248..., 3.4590760... and 5.7423983... are non recurring. We cannot put the bar sign over the decimal place digits of these numbers. We cannot express these decimal numbers as fractions; hence they are irrational numbers.

Dividing Decimals
In this article, we will see how to divide decimals using three scenarios. But before proceeding to the division of decimals, you should know how to convert the decimals into fractions.
For example, to convert 5.34 into a fraction, we will remove the decimal point and add two zeroes in the denominator followed by 1 like this:
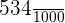
Converting decimals into fractions is a fundamental concept that is very helpful when we are given different scenarios involving decimal numbers either in numerator, denominator or both.
1. Only the Dividend is Decimal
Perform the division of decimal numbers as if they were integers. When the first decimal is lowered, place a decimal point in the quotient and continue dividing.
Examples
1. 526.6562 : 7
In this example, the dividend is 526.6562. The divisor is 7 which is a whole number. Therefore, we will perform the division operation as both the numbers are integers. When we will lower the first decimal place, we will simply place the decimal point in the quotient.

As you can see that when the first decimal place 6 was lowered, we placed a decimal point in the quotient.
2. 83.2 : 16
In this example, 83.2 is a dividend and 16 is a divisor. There is only a single decimal place in the dividend and that is 2. When we will lower 2, we will place the decimal point in the quotient.

2. Only the Divisor is Decimal
Remove the decimal point of the divisor and add to the dividend as many zeros as there are decimal places in the divisor. Then, divide as if they were integers.
Examples
1. 5126 : 62.37
In this example, we will remove the decimal point in the divisor and add two zeros in the dividend. The dividend here is 5126 and the divisor is 62.37. When we will remove the decimal point from the divisor, we will add two zeroes in the dividend because the divisor has 2 decimal places.

The dividend is not completely divisible by the divisor, therefore the remainder is not zero in the above example.
3. The Dividend and the Divider are Decimals
If there are not an equal amount of decimal places in the dividend and divisor, add to the one who has less, as many zeros as there is a difference in the decimal places. Then, divide as if they were integers.
Example
5627.64 : 67.5261
In this example, the dividend is 5627.64 and the divisor is 67.5261. The dividend has less amount of decimal places as compared to the divisor, so we will remove the decimal point from the divisor and add zeroes to the dividend.

Division by the Unit Followed by Zeros
To divide a number by a unit followed by zeros, move the decimal point to the left as many places as there are zeros in the unit.
Examples
1. 
In this example, there is a single zero in the denominator, hence we will move the decimal point one place to the left. The answer will be 23.5
2. 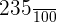
In this example, there are two zeroes in the denominator, therefore we will move the decimal point two places to the left. The final answer is 2.35.
3. 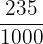
In this example, there are three zeroes in the denominator, hence we will move the decimal point 3 places to the left. The final answer will be 0.235.
4. 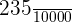
In this example, there are four zeroes in the denominator followed by the unit, therefore we will move the decimal point four places to the left. The final answer will be 0.0235.
Summarise with AI:













If it is (0.0072÷6)
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081