Chapters
Decimal numbers have two parts - an integer or a whole number part which is before the decimal point and the fractional point which is after the decimal point. The decimal point is a period or dot that acts as a separator between the whole number and fractional part. The fractional part of a decimal number is always less than 1. In this article, we will see how to find the square root of a decimal number.
There are many methods to find the square root of a decimal number. Let us see some of the examples below.

Example 1
Solve 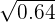
Solution
Remove the decimal point and write the decimal number 0.64 as a fraction like this:
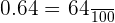
Now, take the square root of the numerator and the denominator separately:
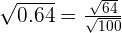
64 is equal to 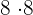 and 100 is equal to
and 100 is equal to 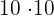 . The resulting fraction will be:
. The resulting fraction will be:
= 
Hence, the answer will be 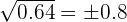
Example 2
Solve 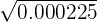
Solution
First, write the decimal number as a fraction like this:
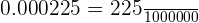
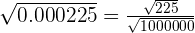
The square root of 225 is equal to 15 and the square root of 1000000 is equal to 1000. Hence, we can write the fraction like this:
= 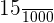
= 0.015
Finding Square Root Using Long Division Method
Finding the square root by converting the decimal numbers into fractions is very easy. However, you may be wondering what happens when you need to find out the square root of a complex number. Well, we can use a long division method to find the square root of the complex decimal number. Let us see some of the examples below.
Example 3
Find the square root of the number 29.16.
Solution
Following steps explain finding the square root of the decimal number 29.16 using a long division method:
Step 1
Write the decimal number and make pairs of integer and fractional parts separately. The pair of the integer part of a decimal number is formed from right to left and the pair of the fractional part is formed right from the start of the decimal point.
For example, in the decimal number 29.16, 29 is the one pair and 16 is another pair.
Step 2
Find the number whose pair is less than or equal to the first pair. In the number 29.16, 5 square is equal to 25. Hence, we will write 5 in the divisor and 5 in the quotient.
Step 3
Now, we will subtract 25 from 29. The answer is 4. We will bring down the other pair which is 16 and put the decimal point in the quotient.
Step 4
Now, we will multiply the divisor by 2. Since 5 into 2 is equal to 10, so we will write 10 _ below the divisor. We need to find out the third digit of the number so that it is completely divisible by the number 416. We already have two digits 10. The third digit should be 4 because 104 . 4 = 116.
Step 5
Write 4 in the quotient's place. Hence, the answer is 5.4.

Example 4
Find the square root of the number 84.64 by a long division method.
Solution
Follow these steps to find the square root of this decimal number 84.64.
Step 1
Write the decimal number and make pairs of integer and fractional parts separately. The pair of the integer part of a decimal number is formed from right to left and the pair of the fractional part is formed right from the start of the decimal point.
Hence, in the decimal number 84.64, 84 is the one pair and 64 is another pair.
Step 2
Find the number whose pair is less than or equal to the first pair. In the number 84.64, 9 square is equal to 81. Hence, we will write 9 in the divisor and 9 in the quotient.
Step 3
Now, we will subtract 81 from 84. The answer is 3. We will bring down the other pair which is 64 and put the decimal point in the quotient after 9.
Step 4
Now, we will multiply the divisor by 2. Since 9 into 2 is equal to 18, so we will write 18 _ below the divisor. We need to find out the third digit of the number so that it is completely divisible by the number 364. We already have two digits 18. The third digit should be 2 because 182 . 2 = 364.
Step 5
Write 2 in the quotient's place after the decimal point. Hence, the answer is 9.2.

Example 5
Find the square root of the number 39.69 by a long division method.
Solution
Follow these steps to find the square root of this decimal number.
Step 1
Write the decimal number and make pairs of integer and fractional parts separately. The pair of the integer part of a decimal number is formed from right to left and the pair of the fractional part is formed right from the start of the decimal point.
Hence, in the decimal number 39.69, 39 is the one pair and 69 is another pair.
Step 2
Find the number whose pair is less than or equal to the first pair. In the number 39.69, 6 square is equal to 36. Hence, we will write 6 in the divisor and 6 in the quotient.
Step 3
Now, we will subtract 36 from 39 which is equal to 3. We will bring down the other pair 69 and put the decimal point in the quotient after 6.
Step 4
Now, we will multiply the divisor by 2. Since 6 into 2 is equal to 12, so we will write 12 _ below the divisor. We need to find out the third digit of the number so that it is completely divisible by the number 369. We already have two digits 12. The third digit should be 3 because 123 . 3 = 369.
Step 5
Write 3 in the quotient's place after the decimal point. Hence, the answer is 6.3.

Example 6
Find the square root of the number 67.826.
Solution
Follow these steps to find the square root of this decimal number.
Step 1
Write the decimal number and make pairs of integer and fractional parts separately. The pair of the integer part of a decimal number is formed from right to left and the pair of the fractional part is formed right from the start of the decimal point. We will add zero after the decimal place values to make it even.
Hence, in the decimal number 67.8260, the pairs are 60, 82 and 60.
Step 2
Find the number whose pair is less than or equal to the first pair. In the number 67.8260, 8 square is equal to 64. Hence, we will write 8 in the divisor and 8 in the quotient.
Step 3
Now, we will subtract 64 from 67 which is equal to 3. We will bring down the other pair 82 and put the decimal point in the quotient after 8.
Step 4
Now, we will multiply the divisor by 2. Since 8 into 2 is equal to 16, so we will write 16 _ below the divisor. We need to find out the third digit of the number so that it is completely divisible by the number 382. There is no three digit number with 16 in it which is completely divisible by 382. So, we will take the number 169. Since, 169 .2 = 338, so we will write 2 after the decimal point at the quotient's place.
Step 5
We will subtract 338 from 382. The answer is 44. The previous divisor was 169. We will form the new divisor by writing 1 as it is and multiplying 69 by 2. Since, 69 . 2 = 138, so the new divisor is 1138.
Step 6
We will take down the last pair 60 and hence the new number is 4460. 4460 is not completely divisible by 1138. Hence, we will find the highest number which is divisible by 1138 but less than 4460. Since, 1138 . 3 = 3414, so we will write 3414 below 4460 and 3 in the quotient's place
Step 7
Subtract 3414 from 4460. The answer is equal to 1046. We will stop the division here.

Find more Maths tuition here on Superprof.













If it is (0.0072÷6)
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081