Decimal numbers have a dot known as a decimal point, which separates their whole number and fractional part. The examples of decimal numbers are 4.14, 3.786, 5.453 and 123.5687. A decimal number can have any number of digits in its decimal places.
The digits after the decimal point are decimal places of the decimal numbers and are ordered in the sequence tenths, hundredths, thousandths, ten-thousandths and so on. The digits before the decimal point are whole numbers and are arranged from right to left in a sequence: unit, ten, hundred, thousand, ten-thousand and so on. Decimal numbers can be divided, multiplied, added or subtracted together. To add or subtract the decimal numbers vertically, they are written in columns with tenths under tenths, hundredths under hundredths and so on. In this article, we will see how to solve the word problems involving decimal numbers.
A water pitcher weighs 0.64 kg when empty and 1.728 kg when filled with water. How much does the water weigh?
It is given that a water pitcher weighs 0.64 kg when empty and 1.728 kg when filled with water. We have to find the weight of the water. To find the weight of the water, we need to subtract the weight when the pitcher is empty from the weight of the pitcher when it is filled with water.

Hence, the weight of the water is 1.088 kg.
A cyclist has travelled 145.8 km in the first stage of a race, 136.65 km in the second stage and 162.62 km in the third.
How many kilometres must the cyclist still complete if the entire race is 1000 km in length?
This example will be solved in two parts. First, we will add the total distance traveled by the cyclist and then we will subtract this traveled distance from 1000 km.

Hence, the total distance traveled by the cyclist is 445.07 km. We have to find the number of kilometers the cyclist still need to travel to complete 1000 km distance. To find the distance left, we will subtract 445.07 from 1000.
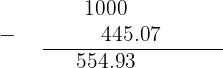
Hence, the cyclist still needs to cover 554.93 km distance.
In a well filled with water, 184.5 litres are removed, followed by 128.75 litres and finally 84.5 litres. After these withdrawals, there are 160 litres in the well. How much water did the well originally have?
To find the amount of water the well originally had, we simply need to add all the numbers together.

Hence, the well originally had 557.75 litres of water.
There are 240 boxes with 25 bags of coffee each. If each bag weighs 0.62 kg, what is the total weight of all the coffee?
To find the total weight of all the coffee, we need to find the weight of an individual box and then multiply this weight by 240. To find the weight of an individual box, we will multiply the weight of a single bag by 25.
Remember that when two decimals or a whole number and decimal number are multiplied together, we ignore the decimal point and multiply them like integers. Once the product is obtained, we count the number of decimal places in both numbers and move the decimal point equal to the decimal places from the left of the final product.

The number of decimal places in 25 is 0 and in 0.67 is 2. The final product obtained is 1550. We will move the decimal point two places to the left of 1550. Hence, each box weighs 15.50 kg.
The next step is to find the weight of 240 boxes. For this, we need to multiply 240 with 15.50.

The number 240 has 0 decimal places and the number 15.50 has 2 decimal places. The total number of decimal places in both numbers is 2. Hence, we will move the decimal point two places to the left of the final product. The final product is 3712000. Moving the decimal point two places to the left will give us the final answer 37120.00 kg.
Knowing that 2.077 m³ of air weighs 2.7 kg, calculate how much 1 m³ of air weighs.
To find the weight of  of air, we need to divide 2.7 by 2.077. In other words, we can say that the dividend is 2.7 and the divisor will be 2.077. Remember that when both the dividend and the divisor are decimal numbers, then we look at the number which has fewer decimal places as compared to the other. We will remove the decimal point from the number which has more decimal places and add zeroes to the other number with fewer decimal places.
of air, we need to divide 2.7 by 2.077. In other words, we can say that the dividend is 2.7 and the divisor will be 2.077. Remember that when both the dividend and the divisor are decimal numbers, then we look at the number which has fewer decimal places as compared to the other. We will remove the decimal point from the number which has more decimal places and add zeroes to the other number with fewer decimal places.
This situation can be written as 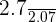 . You can see that the dividend has less number of decimal places, so we will write it as
. You can see that the dividend has less number of decimal places, so we will write it as  .
.
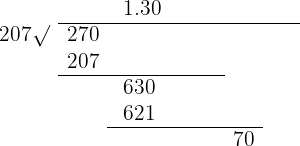
207 is not completely divisible by the number 270, so we will consider the answer 1.30. The weight of  of water is 1.30 kg.
of water is 1.30 kg.
Eva is on a diet which states that she cannot consume more than 600 calories in one meal.
Yesterday she had lunch: 125 g of bread, 140 g of asparagus, 45 g of cheese and an apple of 130 g.
If 1 g of bread has 3.3 calories, 1 g of asparagus, 0.32, 1 g of cheese, 1.2, and 1 g of an apple 0.52.
Did Eva follow her diet?
To answer this question, we need to find the calories in each meal she took yesterday.
The number of calories in 1 g of bread = 3.3
Amount of bread Eva ate = 125
The number of calories in 125 grams of bread = 125 . 3.3
= 412.5 calories
The number of calories in 1g of asparagus = 0.32
Grams of asparagus Eva ate = 140
The number of calories in 140 grams of asparagus = 140 . 0.32
=44.8 calories
The number of calories in 1g of cheese = 1.2
Grams of cheese Eva ate = 45
The number of calories in 45 grams of cheese = 45 . 1.2
=54 calories
The number of calories in 1g of apple = 0.52
Grams of apple Eva ate =130
The number of calories in 130 grams of apple= 130 . 0.52
=67.6 calories
To find the total amount of calories Eva took yesterday, we need to add all the calories together.

It is given that Eva is on diet and she can take no more than 600 calories. The total calories Eva took yesterday were 578.9. Since 578.9 < 600, so yes Eva followed her diet.
James has a rectangular box. The length of the box is 25.78 cm, and its width is 7.16 cm less than its length. What is the area of the rectangle?
First, we need to find out what is required in this question. We need to find out the area of the rectangle. The length is given which is 25.78 cm. The width is 7.16 cm less than its length. Hence, first we need to find out the width of the rectangular box.

Hence, the width of the rectangular box is 18.62 cm. We know that the area of the rectangle is length x width. So, we will multiply the length and width of the rectangular box together to find its area.

Now, we need to count the number of decimal places in both numbers. The number of decimal places in the length is 2, and the number of decimal places in the width of the rectangular box is also 2. Together, these two numbers have 4 decimal places. The final product was 4800236. We need to move the decimal point 4 units to the left.
Hence, the final answer is 480.0236  .
.
Summarise with AI:


If it is (0.0072÷6)
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081
find the square root in decimal form of 6.7081