Chapters
In this article, you will learn what capacity is, what the units of capacity are, and how to convert one unit to another. Let us start by explaining the concept of capacity first.
What is Capacity?
Capacity is the amount of space a container can hold, usually for liquids like water, milk, or juice. It is measured in units such as litres (L) and millilitres (mL).
Example:
A small cup might hold 250 mL of water.
A water bottle might hold 1 L of water.
For instance, the capacity of this well is 108 gallons. It means that the well can hold up to 108 gallons of water. Consider another example below:
A bottle has a capacity of 2 litres. For instance, you put that bottle under the tab and become busy with some other task. What will happen? After some time, when the bottle reaches its full capacity, the remaining water will start overflowing. From this example, you get a lesson that you cannot hold anything in an object beyond its capacity.
How is Capacity Measured?
There are two measurement systems to measure the capacity.
- Customary: This measurement system is used mostly in the United States
- Metric: This measurement is used all around the world
Some interesting facts about customary measurement are given below:
- Gallon, cup, quart, or pint are examples of tools used in customary measurement.
- These measurement tools can be broken down into smaller parts; for instance, a cup can be divided into half, a quarter cup, etc.
- Pints, quarts, and gallons are employed for measuring the capacity of liquids. On the other hand, the measurements such as a tablespoon, teaspoon, and cup are used for measuring liquids other than water, like milk or solids such as sugar.
- The biggest measurement tool in customary measurement is a gallon. The smallest tool is
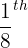of a teaspoon.
Some interesting facts about metric measurement are explained below:
- This measurement is used by all the countries in the world except three. Though in the United States, the customary measurement is used in many places, some places in the U.S use the metric system.
- The commonly used units to measure capacity under metric measurement are litres and millilitres. For instance, you went to a shop and bought 2 litres of water. One millilitre is a 1000th part of a litre.
In this article, we will specifically focus on metric measurements of the capacity.
SI Unit of Capacity Under Metric Measurement
The primary unit for measuring capacity under the metric measurement system is the liter. In other words, it is the standard unit of measurement of capacity. There are also other units for measuring large and small quantities, which are multiples and sub-multiples of litres. The following table shows the bigger and smaller units that are related to litres:
| Kiloliter (kl) | 1000 liters (l) |
|---|---|
| Hectoliter (hl) | 100 liters (l) |
| Decaliter (dal) | 10 liters (l) |
| Deciliter (dl) | 0.1 liter (l) |
| Centiliter (cl) | 0.01liter (l) |
| Milliliter (ml) | 0.001 liter (l) |
Conversion of Units
One unit of capacity can be converted into the other. The problem of converting units to other units becomes an issue of multiplying or dividing the unit by one, followed by as many zeros as there are places between them. In the next section, we will solve a couple of examples in which we will convert one unit of capacity into another.
Convert 80 hl to cl.
Hectoliter (hl) is a bigger unit, and centiliter (cl) is a smaller unit as compared to liter. First, we will convert hectoliters to liters, and then the resulting amount in liters will be converted into centiliters (cl).
1 hectoliter (hl) = 100 liters (l)
80 hl = 80 x 100 litres
= 8000 litres
1 litre = 100 centilitres
8000 litres will be multiplied by 100 to get the centilitres:
8000 litres = 8000 x 100 cl
= 800,000 cl
Hence, 80 hectoliters are equal to 800,000 centilitres.
Convert 3678 centilitres into litres.
Centilitres (cl) is a smaller unit than litres; therefore, we will use the arithmetic operation of division for conversion.
1 litre = 100 centilitre
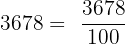litres
Since the value in the numerator is divided by 1 followed by two zeroes, we will move the decimal point 2 units to the left.
= 
litres
Hence, 3678 centilitres are equal to 36.78 litres.
Convert 6500 dal to kl.
Though you can convert the decaliters directly into kiloliters if you know how many decaliters equal kilolitres, it is a good idea to convert decaliters to litres first, and then the resulting amount in litres to kiloliters. Both decaliters (dal) and kiloliters (kl) are bigger units than litres.
1 decaliter (dal) = 10 liters (l)
6500 dal = 6500 x 10 liters
= 65000 litres
1 kiloliter = 1000 litres
65000 liters =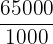 
kl
= 65 kl
Hence, 6500 decaliter is equal to 65 kiloliters.
Convert 205 cl to hl.
Hectoliter (hl) is a bigger unit, and centilitre (cl) is a smaller unit as compared to a litre. First, we will convert centilitres (cl) to litres, and then the resulting amount in litres will be converted into hectoliters (hl).
1 centiliter (cl) = 0.01 liters (l)
205 cl =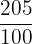 
liters
= 2.05 litres
1 hectoliter = 100 liters
2.05 liters =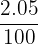 
hl
= 0.0205 hl
Hence, 205 centilitres are equal to 0.0205 hectoliters.
The milkman sold 2400 cl of milk on day 1, 2 litres, 450 millilitres of milk on day 2, and 5 litres, 5 deciliters of milk on day 3. What is the total amount of milk sold by the milkman in litres and millilitres?
This word problem has 2 parts. In the first part, we have to tell the total amount of milk sold in three consecutive days in litres.
Part a)
To answer in litres, first, we have to convert the amount of milk sold on each day into litres and then take an aggregate of the amounts sold in three days.
Amount of milk sold on day 1 = 2400 centiliters (cl)
1 liter = 100 centiliters
2400 cl =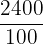 
liters
= 24 litres
Amount of milk sold on day 2 = 2 litres 450 millilitres
In this part, we just need to convert millilitres into litres.
1 liter = 1000 milliliters
450 milliliters =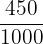 
liters
= 0.45 litres
Total amount of milk sold on day 2 = 2 + 0.45 = 2.45 liters
Amount of milk sold on day 3 = 5 litres, 5 deciliters
Again, we just need to convert 5 deciliters into litres here:
1 liter = 10 deciliter
5 dl =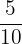 
liters
= 0.5 litres
Total amount of milk sold on day 3 = 5.5 litres
Now, we will add all the amounts together to get the total amount of milk sold on three days.
Total amount of milk sold in liters = 24 + 2.45 + 5.5 = 31.95 liters
Hence, 31.96 litres of milk were sold in three days.
Part b
1 liter = 1000 milliliters
31.95 liters = 31.95 x 1000 ml
= 31950 ml
Hence, 31950 millilitres of milk were sold in three days.
A bigger water tank can hold 64 decaliters of water at a time. There is another smaller tank that can hold 1/4th as much water as the bigger tank. If both tanks are filled to their full capacity, what is the total amount of water in litres present in both tanks?
We need to determine the total amount of water that is present in both water tanks if they are filled to their full capacity.
The capacity of the bigger water tank = 64 dal
The capacity of the smaller water tank =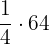 
= 16 dal
Total capacity of both the tanks = 64 + 16 = 80 dal
Amount of water present in both the tanks in liters = 80 x 10 = 800 liters (Remember 1 dal = 10 liters)
Hence, 800 litres of water are present in both tanks.
Did you like this article? Rate it!
Loading...
This is so good as learning !tysm you teach better than my teacher
That cool love that follow God more too💙