Chapters
In this article, we will discuss what is a metric system, how to convert complex measurements into simple measurements, and how to convert simple measurements into complex measurements.
The metric system is an international system of measurements that was first adopted in France in 1795. In the past, every country and in some cases every region were using different units of measurement. This diversity made commercial relations between nations and communities very difficult. In 1792, to resolve these difficulties, the Academy of Sciences in Paris proposed the metric system. This system has been progressively adopted by all countries, with the exception of Burma, Liberia, and the United States. Today, the metric system is used in almost every country except in most parts of the United States, and these three countries.
In the United States, both customary and metric systems are used. In most parts of the world, the metric system is the fundamental system of measurement. In some countries, such as the United Kingdom the metric system coexists with their traditional measurements. If you travel in most of the countries, you will find that the distance is given in kilometers and milk is sold in liters. Kilometer, liter, gram, and meter square are units of the metric system. For smaller and bigger measurements, the metric system offers multiples and submultiples of SI units. For instance, a milliliter is 1000th part of the liter and one liter is equal to 10 deciliters. In other words, we can say that the metric system is based on 10s, unlike the customary measurement system.
The U.S customary system uses feet, quarts, and ounces to measure the length, volume of a liquid, and mass. As we have discussed above that under a metric system the units get smaller or larger with powers of 10. Though customary measurement system is different from the metric one, however, it also has smaller units. For instance, a cup can be broken down into a half, or a quarter cup, etc.

Units of the Metric System
Under the metric system, you will find separate units to the following magnitudes:
The units of time are not part of the metric system. They are related between themselves in a multiple or submultiple of 60. Time is a magnitude of the sexagesimal system.
Complex Measurements
Complex measurements are expressed using different types of units. For example, 3 kg 200 g, 5 km 120 m, and 50 m 22 cm, etc.
Converting Complex Measurements to Simple Measurements
You can convert complex measurements into simple measurements. In the following examples, you will learn how to do so.
Example 1
Convert 13 km 5 dam 42 m in a simple measurement (cm).
Solution
To convert the above complex measurement into a cm, we will separately convert each part into cm.
1 km = 1000 meters
1m = 100 cm
1 km = 100,000 cm
Since kilometer is a bigger unit and centimeter is a smaller one, therefore we will multiply 13 km with 100,000 to convert it into cm:
13 = 13 x 100,000
=1300,000 cm
Now, we will convert 15 dam into cm:
1 dam = 10 m
1m = 100 cm
1 dam = 1000 cm
Again, decameter (dam) is a bigger unit and centimeter (cm) is a smaller one, therefore we will use the operation of multiplication here:
5 dam = 5000 cm
Now, we will convert the last part which is in meter into centimeters:
1 m = 100 cm
42 m = 42 x 100 = 4200 cm
To write the final measurement, we will add up all these three measurements like this:
1200, 000 + 5000 + 4200 = 1209200 cm
Example 2
The shop sold 1800 cl 200 ml of milk on day 1, 8 liters 850 milliliters of milk on day 2, and 13 liters 20 deciliters of milk on day 3. Give the total amount of milk sold the milkman in liters and milliliters.
Solution
There are two parts in this problem. In the first part, we have to convert all the complex measurements to liters and add them up and in the next part we will convert liters of milk into milliliters.
Part a
To answer in liters, first, we have to convert the amount of milk sold on each day into liters and then take an aggregate of the amounts sold in three days.
Amount of milk sold on day 1 = 1800 cl 200 ml
1 liter = 100 centiliters
1800 cl = 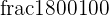 liters
liters
= 18 liters
1 liter = 1000 ml
200 ml = 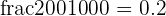 liters
liters
Total amount of milk sold on day 1 (in simple measurement) = 18 + 0.2 = 18.2 liters
Amount of milk sold on day 2 = 8 liters 850 milliliters
In this part, we just need to convert 850 milliliters into liters.
1 liter = 1000 milliliters
850 milliliters = 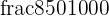 liters
liters
= 0.85 liters
Total amount of milk sold on day 2 = 8 + 0.85 = 8.85 liters
Amount of milk sold on day 3 = 13 liters 20 deciliters
Again, we just need to convert 20 deciliters into liters here:
1 liter = 10 deciliter
20 dl =  liters
liters
= 2 liters
Total amount of milk sold on day 3 (in simple measurements) = 13 + 2 = 15 liters
Now, we will add all the amounts together to get the total amount of milk sold on three days.
Total amount of milk sold in liters = 18.2 + 8.85 + 15 = 42.05 liters
Hence, 42.05 liters of milk was sold in three days.
Part b
In this part, we will simply convert the liters into milliliters:
1 liter = 1000 milliliters
Since liters is a bigger unit and milliliters is a smaller one, therefore, we will use the operation of multiplication here:
42.05 liters = 42.05 x 1000 ml
= 42050 ml
Hence, 42050 milliliters of milk was sold in three days.
Simple Measurements
Simples measurements are expressed using only one type of unit. For example, 3.2 kg, and 5.12 m.
Converting Simple Measurements to Complex Measurements
There are two cases:
- To convert to larger numbers, the division is used.
- To convert to smaller numbers, the multiplication is used.
In the next section, we will solve two examples considering the above scenarios.
Example 1
Convert 6418 mm into complex measurements.
Solution
6418 is a larger number which can be divided into different units like this:
First, we will divide 6418 by 1000. The remainder will be 418 and the quotient is 6. Remember that 1000 mm is equal to 1 meter. So, 6000 mm is equal to 6 meters.
Now, we will divide 418 by 100. The quotient will be 4 and the remainder is 18. 100 mm is equal to 10 decimeters. So, 400 mm is equal to 4 dm.
In this step, we will divide 18 by 10. 10 mm is equal to 1 cm.
The remainder 8 has only one digit, so it is millimeter.
From the above steps, we can write the measurement 6418 mm into complex measurement as:
6418 mm = 6 m 4 dm 1 cm 8 mm
Example 2
Convert 2.685 km into a complex measurement.
Solution
In 2.685 km the unit of the digit before the decimal place is straightforward. It is 2 km. The number after decimal place is 0.685.
0.685 has three digits after the decimal place, so we will multiply it by 1000.
= 0.685 x 1000 = 685
Hence, 2.685 km is equal to 2 km 685 m.
Summarise with AI:













This is so good as learning !tysm you teach better than my teacher
That cool love that follow God more too💙