Chapters

What is Volume?
Volume is the amount of space occupied by a 3D object.
Formula for volume of a cuboid:
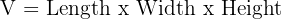
Volume is always expressed in cubic units.
Example
A tank has length = 7 ft, width = 2 ft, height = 5 ft. The volume is:
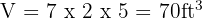
Units of Volume
A unit of volume measures the amount of three-dimensional space an object, liquid, or gas occupies. In the metric system, volume units are standardised and based on powers of ten, making them simple to convert. These volume units are widely used in science, engineering, cooking, and everyday life.
The standard unit
- The official SI volume unit is the cubic metre (m³), defined as the volume of a cube with sides of 1 metre.
- Because this unit of volume is quite large for most everyday uses, the litre (L) is commonly used for liquids and smaller capacities.
| Volume Unit | Symbol | Meaning | Relation to other units |
|---|---|---|---|
| cubic metre | m³ | A cube 1 m × 1 m × 1 m | 1 m³ = 1,000 litres |
| litre | L | Equal to one cubic decimetre (1 dm³) | 1 L = 1 dm³ = 1,000 cm³ |
| millilitre | mL | One thousandth of a litre | 1 mL = 0.001 L = 1 cm³ |
The SI base unit of volume is the cubic metre (m³).
Larger and smaller units (km³, cm³, mm³, etc.) are multiples of the cubic metre.
Conversion rule: To move between units, multiply or divide by 1000 for each step.
| Unit (Volume) | Symbol | Equivalent in m³ |
|---|---|---|
| Cubic kilometre | km³ | 1000000000 |
| Cubic hectometre | hm³ | 1000000 |
| Cubic decametre | dam³ | 1000 |
| Cubic metre (SI) | m³ | 1 |
| Cubic decimetre | dm³ | 0.001 |
| Cubic centimetre | cm³ | 0.000001 |
| Cubic millimetre | mm³ | 0.000000001 |
Metric prefixes for volume units
Metric prefixes can be added to litres (and other volume units) just like other measurements such as length or mass:
- 1 kL (kilolitre) = 1,000 L
- 1 hL (hectolitre) = 100 L
- 1 dL (decilitre) = 0.1 L
- 1 cL (centilitre) = 0.01 L
Useful conversions between volume units
- 1 m³ = 1,000 L
- 1 L = 1 dm³
- 1 mL = 1 cm³
- 1 km³ = 1,000,000,000 m³
Why understanding volume units matters
Learning how to convert between each unit of volume helps in everyday and professional contexts. Whether you’re measuring liquids for cooking, calculating the capacity of containers, or performing scientific experiments, mastering volume units ensures accuracy and consistency. The metric system’s base-ten structure makes converting between volume units simple—just move the decimal point!
Relationship Between Volume, Capacity, and Mass
Capacity is the amount that a 3D object can contain.
Volume and capacity are closely linked:
- 1 litre (L) = 1 dm³
- 1 millilitre (mL) = 1 cm³
- For pure water at 4 °C: 1 g = 1 cm³ = 1 mL
| Capacity | Volume | Mass of water |
|---|---|---|
| 1 kilolitre (kL) | 1 m³ | 1 tonne (t) |
| 1 litre (L) | 1 dm³ | 1 kilogram (kg) |
| 1 millilitre (mL) | 1 cm³ | 1 gram (g) |
Practice Questions with Solutions
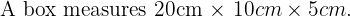
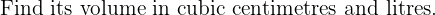
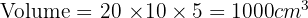
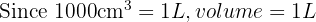
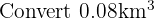
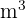
We know that:
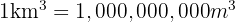
Therefore:
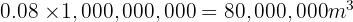
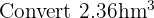
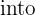
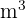
We know that:
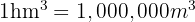
Therefore:
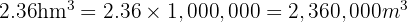
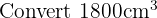
We know that:
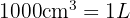
Therefore:
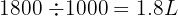
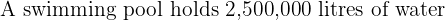
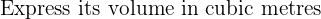
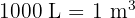
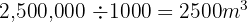
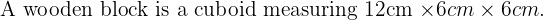
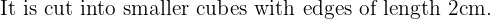
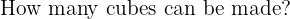

The volume of the cuboid is:
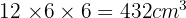
The volume of one cube is:
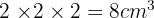
The number of cubes =
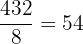
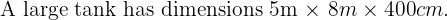
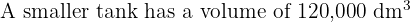
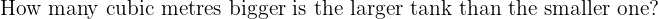
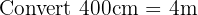
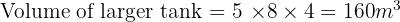
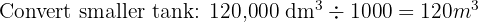
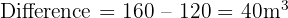












This is so good as learning !tysm you teach better than my teacher
That cool love that follow God more too💙