In physics and mathematics, measuring physical quantities accurately is essential. The metric system is the international standard used by almost every country in the world (including the UK for most scientific and mathematical purposes) to ensure consistency.
Before this system was adopted in France in 1795, different regions used different measurements, making trade and communication difficult. Today, the metric system solves this by using a base-10 structure. This means that smaller and larger units are related by powers of 10, making calculations straightforward.
What is Length? Length is defined as the distance between two points, or the maximum extended dimension of an object.
The fundamental SI (International System of Units) unit for length is the metre (m).

Metric Units of Length
While the metre is the standard unit, we often need to measure things much smaller (like an ant) or much larger (like the distance between cities). For this, we use prefixes.
Here are the most common metric units of length, ordered from largest to smallest:
| Unit | Symbol | Value in Metres | Typical Use |
|---|---|---|---|
| Kilometre | km | 1000 m | Roads and geography |
| Hectometre | hm | 100 m | Land measurement |
| Decametre | dam | 10 m | Surveying |
| Metre | m | 1 m | Everyday objects and height |
| Decimetre | dm | 0.1 m | Educational contexts |
| Centimetre | cm | 0.01 m | Body measurements and furniture |
| Millimetre | mm | 0.001 m | Engineering and small tools |
| Micrometre (Micron) | μm | 0.000001 m | Cells and bacteria |
| Nanometre | nm | 0.000000001 m | Light wavelengths |
| Angstrom | Å | 0.0000000001 m | Atoms and molecules |
Key Conversion Rules:
- Big to Small: To convert a larger unit to a smaller one (e.g., km to m), you multiply by the conversion factor (10, 100, 1000, etc.).
- Small to Big: To convert a smaller unit to a larger one (e.g., mm to cm), you divide by the conversion factor.
Practice Questions & Solutions
A bookshelf is 1.2 metres wide. Calculate the width of the bookshelf in:
- Centimetres (cm)
- Millimetres (mm)
1. There are 100 cm in 1 metre. Multiply by 100:
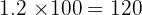
Answer: 120 cm
2. There are 1000 mm in 1 metre. Multiply by 1000:
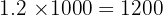
Answer: 1200 mm
James drives a distance of 45.6 kilometres. How many metres did he drive?
We are converting from km to m (large to small). Factor: 1 km = 1000 m.
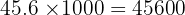
Answer: 45,600 m
A beetle is 35 millimetres long. Express this length in metres.
We are converting from mm to m (small to large). Factor: 1 m = 1000 mm. We divide by 1000:
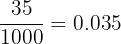
Answer: 0.035 m
A construction project requires three pieces of pipe with the following lengths: 2 metres, 80 centimetres & 1500 millimetres. Calculate the total length of the pipe required in metres.
First, convert all units to metres.
Piece 1: 2 m (already in metres).
Piece 2 (80 cm): Divide by 100.
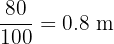
Piece 3 (1500 mm): Divide by 1000.
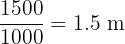
Now, add them together:
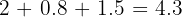
Answer: 4.3 m
Sarah has a ribbon that is 450 centimetres long. She needs to cut it into smaller strips that are each 0.5 metres long. How many full strips can she cut from the ribbon?
First, make the units the same. Let's convert the ribbon length to metres. Divide cm by 100:
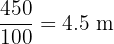
Now, divide the total length by the length of one strip:
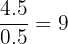
Answer: 9 strips












This is so good as learning !tysm you teach better than my teacher
That cool love that follow God more too💙