Whenever we multiply numbers, what we are doing is adding equal groups of a number. For example, if we multiply two times five, this means the group is two and we will be adding that group five times which will be equal to ten. Multiplication is known as one of the basic math operations. In fact, it helped us by reducing the number of steps as well as the chances of error. Without multiplication, finding solutions might become impossible and not to mention the chances of error.
To multiply two natural numbers, you need two natural numbers and then add one factor to itself many times as indicated by the other factor. Suppose you have two natural numbers, one is  another is
another is  . Now you need to add
. Now you need to add 
 times to get the answer. In mathematical language, this would be
times to get the answer. In mathematical language, this would be 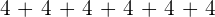 which is equal to
which is equal to  . We call this multiplication of natural numbers. The syntax of the multiplication of two natural numbers is:
. We call this multiplication of natural numbers. The syntax of the multiplication of two natural numbers is:
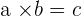
The terms a and b are called factors and the result, c, is the product. Whenever you see "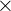 " sign, that indicates multiplication. Sometimes it is written in form of brackets, like this
" sign, that indicates multiplication. Sometimes it is written in form of brackets, like this 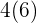 which also means multiplication. When you multiply two natural numbers, the result will always be a natural number.
which also means multiplication. When you multiply two natural numbers, the result will always be a natural number.

Properties of the Product of Natural Numbers
Property No.1: Closure
This property tells that if you multiply two natural numbers this will result in a new number which will also be a natural number.
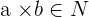
Property No.2: Associative
It doesn't matter what way you group, it will always result in the same. In simple words, the way in which the factors are grouped does not change the result.

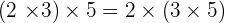

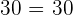
Property No.3: Commutative
When you are multiplying two natural numbers, the order doesn't change the product.


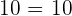
Property No.4: Multiplicative Identity
The  is the neutral element of the multiplication because any number multiplied by it gives the same number.
is the neutral element of the multiplication because any number multiplied by it gives the same number.
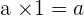
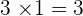
Property No.5: Distributive
The multiplication of a natural number and a sum is equal to the sum of the multiplication of the natural number for each of the addends.
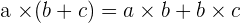
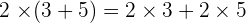
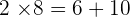
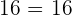
Removing a common factor:
It is the reverse of the distributive property.
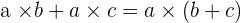
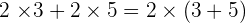
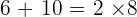
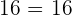
Summarise with AI:













I’m afraid this article (on cardinal numbers) has an unfortunate error. Zero must be considered a cardinal number. The definition of a cardinal number given by the Penguin Dictionary of Mathematics is “A number that indicates the number of elements in a set.” It also defines a null set or empty set containing no elements. The cardinality of this set is 0.