Chapters
- Exercise 1.
- Exercise 2.
- Exercise 3.
- Exercise 4.
- Exercise 5.
- Exercise 6.
- Exercise 7.
- Exercise 8.
- Exercise 9.
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
Exercise 1.
Look for the term unknown and indicate its name in the following operations:
1.
2.
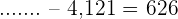
3.
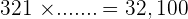
4.
Exercise 2.
Look for the term unknown in the following operations:
1.
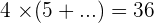
2.
3.
4.
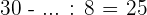
Exercise 3.
Calculate two different ways of completing the following operations:
1.
2.
3.
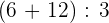
Exercise 4.
Remove the common factor:
1.
2.
3.
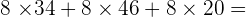
Exercise 5.
Express the following numbers in powers:
1.
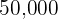
2.
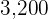
3.
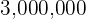
Exercise 6.
Calculate:
1.
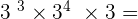
2.
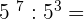
3.
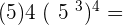
4.
5.
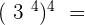
6.
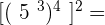
7.
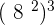
8.
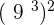
9.
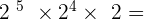
10.
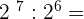
11.
12.
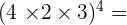
13.
14.
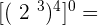
15.
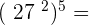
16.
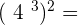
Exercise 7.
Using powers, carry out the polynomial decomposition of these numbers:
1.
2.
3.
Exercise 8.
Calculate the square roots:
1.
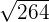
2.
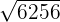
3.
Exercise 9.
Calculate:
1.
2.
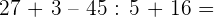
3.
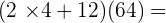
4.
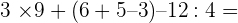
5.
6.
7.
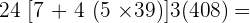
8.
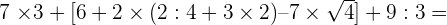
Solution of exercise 1
Look for the unknown term and indicate its name in the following operations:
1.
addend.
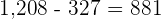
2.
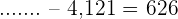
Minuend.
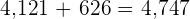
3.
Factor.
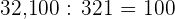
4.
Divisor.
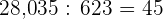
Solution of exercise 2
Look for the unknown term in the following operations:
1.
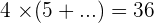
2.
3.
and 
4.
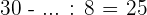
Solution of exercise 3
Calculate two different ways of completing the following operations:
1.
2.
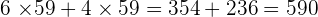
3.
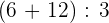
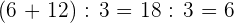
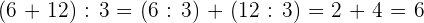
Solution of exercise 4
Remove the common factor:
1.
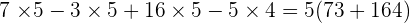
2.
3.
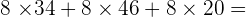
Solution of exercise 5
Express the following numbers in powers:
1.
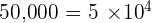
2.
3.
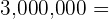
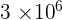
Solution of exercise 6
Calculate:
1.
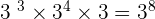
2.
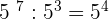
3.
4.
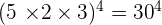
5.
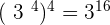
6.
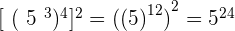
7.
8.
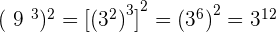
9.
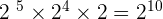
10.
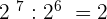
11.
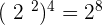
12.
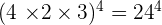
13.
14.
15.
16.
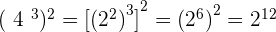
Solution of exercise 7
Using powers, carry out the polynomial decomposition of these numbers:
1.
2.
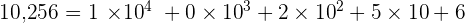
3.
Solution of exercise 8
Calculate the square roots:
1.
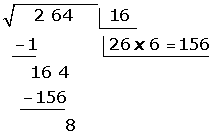
2.
3.
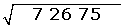
Solution of exercise 9
Calculate:
1.
2.
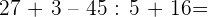
3.
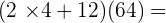
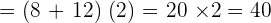
4.
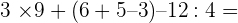
5.
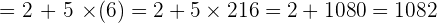
6.
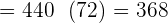
7.
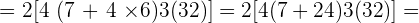
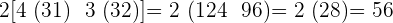
8.
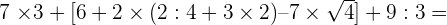
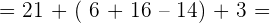
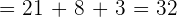
Summarise with AI:
Did you like this article? Rate it!
Loading...
I’m afraid this article (on cardinal numbers) has an unfortunate error. Zero must be considered a cardinal number. The definition of a cardinal number given by the Penguin Dictionary of Mathematics is “A number that indicates the number of elements in a set.” It also defines a null set or empty set containing no elements. The cardinality of this set is 0.