To understand numbers, mathematicians have categorized numbers into different types. These types include integers, whole numbers, decimals, rational numbers, and many more. One of them is Natural Numbers. These categories help us in many ways from engineering aspects to research aspects. The question is what are natural numbers and how can we identify natural numbers? Keep on reading.

Definition
The basic definition of natural numbers is that they are positive whole numbers ranging from zero to positive infinity. If we break down the definition, there are two conditions on which you can declare whether the number is a natural number or not. The first condition is that they should be positive numbers. This means that all negative numbers (which include a negative sign such as 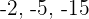 , etc.) are not natural numbers. Hence, if you see a negative number, whether that negative number is a whole number or not, it is not a natural number for sure. The second condition is that they are whole numbers. This means that natural numbers are perfect numbers such as
, etc.) are not natural numbers. Hence, if you see a negative number, whether that negative number is a whole number or not, it is not a natural number for sure. The second condition is that they are whole numbers. This means that natural numbers are perfect numbers such as 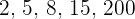 , etc. If you see any decimal number or fraction number, they won't be counted in natural numbers because decimal or fraction numbers are not perfect numbers. Last but not least, Natural numbers count the elements of a whole, a cardinal number, or express the order which occupies an element in a whole, ordinal number.
, etc. If you see any decimal number or fraction number, they won't be counted in natural numbers because decimal or fraction numbers are not perfect numbers. Last but not least, Natural numbers count the elements of a whole, a cardinal number, or express the order which occupies an element in a whole, ordinal number.
Comparison and Ordering Natural Numbers
In addition, natural numbers are also in order. It means that they are not random numbers, in fact, they have an ascending order. This allowed us to compare two natural numbers. To order them, you need to select two natural numbers. For example, we took  , and
, and  . To compare them, we use two special signs and they are "greater than" (
. To compare them, we use two special signs and they are "greater than" (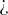 ) and "lesser than" (
) and "lesser than" (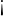 ) signs. The greater-than sign means that the left-hand side number is greater than the right-hand side number. On the other hand, the lesser than sign means that the left-hand side number is lesser than the right-hand side number. Let's get back to our example, now we need to compare both numbers. Since number
) signs. The greater-than sign means that the left-hand side number is greater than the right-hand side number. On the other hand, the lesser than sign means that the left-hand side number is lesser than the right-hand side number. Let's get back to our example, now we need to compare both numbers. Since number  is lesser than the number
is lesser than the number  , you write like this,
, you write like this, 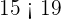 . Pretty simple right? Instead of writing lesser than or greater than every time, we use these symbols which saves a lot of time, and visually they are very clear to understand. Below are some more examples of comparison between two natural numbers.
. Pretty simple right? Instead of writing lesser than or greater than every time, we use these symbols which saves a lot of time, and visually they are very clear to understand. Below are some more examples of comparison between two natural numbers.
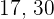
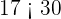
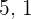
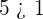
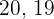
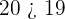
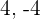
The solution is unavailable because  is not a natural number, it is an integer and this topic only covers natural numbers.
is not a natural number, it is an integer and this topic only covers natural numbers.
The key points to remember are that natural numbers are positive whole numbers. There are unlimited numbers in maths, does this means that infinity is also a natural number? If the infinity is positive then you can say it is a natural number. In simple words, natural numbers are unlimited. If you add  to any natural number, you will get another natural number. For example, zero is a natural number, if we add one to zero, the result will be one which is also a natural number.
to any natural number, you will get another natural number. For example, zero is a natural number, if we add one to zero, the result will be one which is also a natural number.
Representation of the Natural Numbers
The natural numbers can be represented in a straight line ordered from minor to major.
On a straight line, draw one point and mark it with the number zero. To the right of the zero, and with the same separations, place in ascending order the following natural numbers: 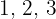 ...
...

Summarise with AI:













I’m afraid this article (on cardinal numbers) has an unfortunate error. Zero must be considered a cardinal number. The definition of a cardinal number given by the Penguin Dictionary of Mathematics is “A number that indicates the number of elements in a set.” It also defines a null set or empty set containing no elements. The cardinality of this set is 0.