Every number has power. It doesn't matter whether you are dealing with natural numbers or any other type of number, it will always have power. Power is an abbreviated form of writing a multiplication formed by several equal factors.
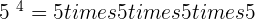
At this point, you might be wondering how come every number has power? To understand this, let's pick a number. For example, imagine the number  . Can we write
. Can we write  like this "
like this "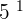 "? Of course yes! Because power is basically multiplication, since we are dealing with
"? Of course yes! Because power is basically multiplication, since we are dealing with  that means
that means  is multiplied once. Power can be in negative as well as in a fraction or decimal form but one thing is for sure and that is every number has power. A number without power is unity. It doesn't matter whether it is ten million or a hundred billion, if their powers are zero, they will become unity. When you are dealing with powers in mathematics, you will come across two things and they are base and exponent.
is multiplied once. Power can be in negative as well as in a fraction or decimal form but one thing is for sure and that is every number has power. A number without power is unity. It doesn't matter whether it is ten million or a hundred billion, if their powers are zero, they will become unity. When you are dealing with powers in mathematics, you will come across two things and they are base and exponent.

Base
The base of power is the number that multiplies by itself. In the above example, base is  because if you notice,
because if you notice,  is been multiplied by itself and that is why we call it base.
is been multiplied by itself and that is why we call it base.
Exponent
The exponent of power indicates the number of times to multiply the base by itself. In the above example, exponent is  because
because  is been multiplied
is been multiplied  times and that is why we call it exponent.
times and that is why we call it exponent.
Properties of the Powers of Natural Numbers
Property No.1: Zero Power
Any number whose power is equal to zero will always result in unity. Neither sign nor the absolute value matters, once the power is reduced to zero, the answer will always be  .
.

a0 = 1
Property No.2: Standard Power of Any Number
Every number has power. If you see a number that doesn't mention a power that means it has a power of  . Hence, every number has a power of
. Hence, every number has a power of  .
.
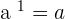
Property No.3: Product of powers with the same base
If there is a multiplication sign and the numbers are the same having different powers then you can add both powers. In other words, it is another power with the same base and the exponent is the sum of the exponents.
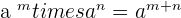
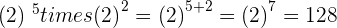
Property No.4: Division of powers with the same base
If there is a division sign and the numbers are the same having different powers then you can subtract both powers. In other words, it is another power with the same base and the exponent is the difference of the exponents.
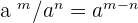
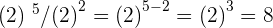
Property No.5: Power of a power
It is another power with the same base and the exponent is the product of the exponents.


Property No.6: Multiplication of powers with the same exponent
If the bases are different but the power of both bases are the same with a multiplication sign then you can write them in a group and then apply the multiplication operation. In other words, It is another power with the same exponent, whose base is the product of the bases.
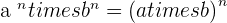
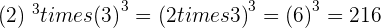
Property No.7: Division of powers with the same exponent
If the bases are different but the power of both bases are the same with a division sign then you can write them in a group and then apply the division operation. It is another power with the same exponent, whose base is the quotient of the bases.


Polynomial Decomposition of a Number
A natural number can be decomposed using powers with the base of 10.
The number 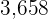 can be decomposed as follows:
can be decomposed as follows:
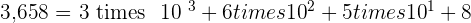
Negative Exponents, Fractional Exponent, Exponents Worksheets.
Summarise with AI:













I’m afraid this article (on cardinal numbers) has an unfortunate error. Zero must be considered a cardinal number. The definition of a cardinal number given by the Penguin Dictionary of Mathematics is “A number that indicates the number of elements in a set.” It also defines a null set or empty set containing no elements. The cardinality of this set is 0.